[題組:第3-4題]
假設棒球的旋轉與空氣阻力可被忽略，回答第3-4題有關棒球的問題。
某職棒投手先以固定力將靜止的棒球沿直線帶動約 1.5 m 的長度後，投出 144 km/h 的快速直球。已知棒球的質量約為 150 g，則該投手施於球的固定力量值約為何？
(A) 80 N
(B) 100 N
(C) 110 N
(D) 120 N
(E) 130 N。
答案
運動學
110指考物理分科考科_04
[題組:第3-4題]
棒球抵達本壘板上方時，在離地 1.0 m 的高度，被打擊者以與水平面夾角為 \( \theta (\cos \theta = \frac{3}{5}) \) 的仰角，量值為 126 km/h 的速度反向擊出，該球在被擊出後 5.0 s 恰好飛越全壘打牆的上空，試問球飛越全壘打牆瞬間，離地高度為多少 m？（假設棒球場地面為水平，取重力加速度 \( g = 10 \text{m/s}^2 \)）
(A) 4
(B) 8
(C) 10
(D) 12
(E) 16。
答案
略解：\( v_0 = 126 \text{km/h} = 35 \text{m/s} \)，\( \cos \theta = \frac{3}{5} \)，\( \sin \theta = \frac{4}{5} \)。
鉛直位移：\( y = v_{0y} t - \frac{1}{2}gt^2 = 35 \times \frac{4}{5} \times 5 - \frac{1}{2} \times 10 \times 5^2 = 140 - 125 = 15 \text{m} \)。
離地高度：\( 1.0 + 15 = 16 \text{m} \)。
答案：E
111物理分科測驗–03
一部汽車以等速度10.0m/s沿水平車道前行，駕駛發現前方24.5m處的單車沿同一直線與方向前進，於是立刻煞車而以等加速度-a繼續前行。若單車一直以等速度3.00m/s前進，而兩車不會相撞，則a至少約需大於下列何者？注：在等速度運動的坐標系中，牛頓運動定律都能成立。
(A) \(\frac{(10.0)^2}{2 \times 24.5} m/s^2 = 2.04m/s^2\)
(B) \(\frac{[(10.0)^2 – (3.00)^2]}{2 \times 24.5} m/s^2 = 1.86m/s^2\)
(C) \(\frac{(10.0 – 3.00)^2}{2 \times 24.5} m/s^2 = 1.0m/s^2\)
(D) \(\frac{[(10.0)^2 – 2 \times 10.0 \times 3.00]}{2 \times 24.5} m/s^2 = 0.82m/s^2\)
(E) \(\frac{[(10.0)^2 – 2 \times 10.0 \times 3.00]}{24.5} m/s^2 = 1.64m/s^2\)
答案
112物理分科測驗–06
某一雜技表演者用五顆相同的小球做單手拋球表演，由同一高度依次將各球略微偏離鉛直方向、向上拋出，當球回到原本被拋出的高度時，以同一隻手將球接住，然後水平移動到拋出點，再拋出，如圖1所示的逆時針軌跡。每次拋球的時間間隔固定為 \( \tau \)，初速的鉛直分量皆為 \( v_0 \)，各球的運動軌跡相同，形成連續的循環。過程中，在空中而不在手中的球至少有四顆。假設重力加速度的量值為 \( g \)，且空氣阻力可忽略，則下列選項何者正確？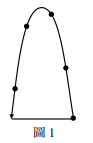
(A) \( v_0 \) 可以是 \( \frac{g\tau}{2} \)
(B) \( v_0 \) 可以是 \( g\tau \)
(C) 每一小球在空中的時間可以是 \( 3\tau \)
(D) 小球在最高點時離拋出點的鉛直距離可以是 \( \frac{g\tau^2}{2} \)
(E) 小球在最高點時離拋出點的鉛直距離一定大於 \( 2g\tau^2 \)
答案
空中至少 4 顆球，故每球在空中時間 \( t \) 滿足 \( 4\tau < t < 5\tau \)。鉛直上拋 \( t = \frac{2v_0}{g} \)，故 \( 2g\tau < v_0 < \frac{5}{2}g\tau \)，(A)(B)錯。\( t \) 不在 \( 3\tau \) 範圍，(C)錯。最高點 \( h = \frac{v_0^2}{2g} = \frac{g}{2}(\frac{t}{2})^2 \)，代入 \( t \) 範圍得 \( 2g\tau^2 < h < \frac{25}{8}g\tau^2 \)，(D)錯(E)對。
112物理分科測驗–13
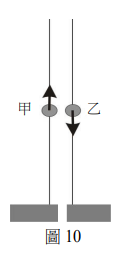
甲、乙兩顆大小相同但質量不同的均勻小球，自同一高度以不同的初速水平拋出，落在平坦的地面上。已知甲球的質量為乙球的 4 倍，但甲球的初速為乙球的一半。若不計空氣阻力，則下列敘述何者錯誤？
(A)乙球的水平射程較大
(B)兩球在空中的飛行時間相等
(C)落地前瞬間，乙球的動能較大
(D)落地前瞬間，兩球的加速度相等
(E)落地前瞬間，兩球速度的鉛直分量相等
答案
114物理分科測驗06
小角度的單擺擺動可視為簡諧運動。一個擺長0.20m的單擺作小角度的左右來回擺動，當擺鐘由左向右經過平衡位置時開始計時，經過1.5s後，下列關於單擺運動狀況的敘述何者正確？（取重力加速度為9.8m/s²）
(A)擺鐘向左運動且速率增加 (B)擺鐘向左運動且速率減少
(C)擺鐘向右運動且速率減少 (D)擺鐘向右運動且速率增加
(E)擺鐘向左作等速運動
答案
114物理分科測驗08
電子與帶 +n 價的離子之質量分別為 m 與 M，各自在相同均勻磁場中作等速圓周運動，其角頻率分別為 \( \omega_m \) 與 \( \omega_M \)。試問其角頻率之比 \( \omega_m / \omega_M \) 為下列何者？
(A) \( \frac{m}{M} \) (B) \( \frac{m}{nM} \) (C) \( \frac{M}{nm} \) (D) \( \frac{nm}{M} \) (E) \( \frac{nM}{m} \)
答案
114學測自然考科23
[題組:第22題到第23題]
太空船停在地球表面上所發出的電磁波由地球監控站測得的頻率為\(f_0\)。若太空船飛行過程，從地球監控站所測得的電磁波頻率為\(f\)，則下列過程的頻率關係，哪些正確？（應選2項）
(A)加速過程\(f < f_0\)
(B)加速過程\(f = f_0\)
(C)等速過程\(f = f_0\)
(D)等速過程\(f < f_0\)
(E)減速過程\(f > f_0\)
105學測自然試題-30
將一個小球從地面鉛直上拋，假設空氣阻力可以忽略。圖 10 中甲時刻和乙時刻分別對應於小球往上升及往下掉的過程中，在任一相同高度處的運動狀態，則下列有關小球於甲、乙兩時刻對應的物理量，哪些一定相同？（應選 3 項）
(A)甲、乙兩時刻的加速度
(B)甲、乙兩時刻的速度
(C)甲、乙兩時刻的重力位能
(D)甲、乙兩時刻的動能
(E)從地面至甲時刻的時間與自最高點掉落至乙時刻的時間
答案
105學測自然試題-46
質量為50 kg的某生站在電梯內的體重計上，電梯原靜止於第一樓層，電梯起動後最初10 s體重計的讀數均為60 kgw，之後20 s體重計的讀數均為45 kgw。若取重力加速度為10 m/s²，則電梯經過30 s的位移為多少m？
(A) 100 (B) 150 (C) 200 (D) 250 (E) 300
答案
體重計讀數反映視重N。質量m=50 kg。重力mg=500 N。
0~10 s: N=60 kgw = 600 N > mg，超重，加速度a₁向上。N - mg = ma₁， 600-500=50a₁， a₁=2 m/s²向上。初速0，位移s₁=0*10 + ½*2*10²=100 m，末速v₁=0+2*10=20 m/s向上。
10~30 s: N=45 kgw = 450 N < mg，失重，加速度a₂向下。mg - N = ma₂， 500-450=50a₂， a₂=1 m/s²向下。時間Δt=20 s。位移s₂ = v₁Δt + ½a₂Δt² = 20*20 + ½*(-1)*20² = 400 - 200 = 200 m。總位移s = s₁ + s₂ = 100 + 200 = 300 m。答案：(E)