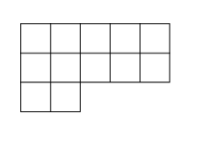
一個房間的地面是由 12 個正方形所組成,如右圖。
今想用長方形瓷磚舖滿地面,已知每一塊長方形瓷磚可以覆蓋兩個相鄰的正方形,即
或
。則用 6 塊瓷磚舖滿房間地面的方法有 \(~~~~~~~~~~~\) 種。
[選填]
答案
原圖形由兩個 \(2 \times 3\) 矩形組成。分兩類討論如下:
---
**① 排出兩個 \(2 \times 3\) 矩形:**
在 \(4 \times 3\) 方格中,排出一個 \(2 \times 3\) 矩形有 \(3\) 種方法;
對每種排法,在剩下的區域排出另一個 \(2 \times 3\) 矩形也有 \(3\) 種方法。
由乘法原理得:
\[
3 \times 3 = 9 \text{ 種}。
\]
---
**② 沒有排出 \(2 \times 3\) 矩形:**
此類排法根據圖示(未附)共有 \(2\) 種方法。
---
總方法數為:
\[
9 + 2 = 11 \text{ 種}。
\]