設圓 \(O\) 之半徑為 24,\(OC = 26\),\(OC\) 交圓 \(O\) 於 \(A\) 點,\(CD\) 切圓 \(O\) 於 \(D\) 點,\(B\) 為 \(A\) 點到 \(OD\) 的垂足,如右邊的示意圖。則 \(AB = \boxed{\frac{120}{13}}\)。
答案
切線
105學測數學考科–C
從橢圓Γ的兩焦點分別作垂直於長軸的直線，交橢圓於四點。已知連此四點得一個邊長為2的正方形，則Γ的長軸長為 __________。
答案
設橢圓長軸在x軸上，中心原點。焦點 \( F_1(-c,0), F_2(c,0) \)。過焦點作垂直長軸的直線 \( x=\pm c \)，與橢圓交點縱坐標為 \( \pm \frac{b^2}{a} \)。正方形邊長2 ⇒ \( \frac{2b^2}{a} = 2 \Rightarrow b^2 = a \)。又 \( c^2 = a^2 - b^2 \)，且由圖形及畢氏定理，點 \( (c, \frac{b^2}{a}) \) 到 \( F_2 \) 距離為 \( \sqrt{0^2 + (\frac{b^2}{a})^2} = \frac{b^2}{a} = 1 \)。代入得 \( b^2=1 \)，\( a=1 \)，\( c=0 \) 不合。修正：由圖形點 \( (c,1) \) 在橢圓上，滿足 \( \frac{c^2}{a^2} + \frac{1}{b^2} = 1 \)，且 \( a^2 = b^2 + c^2 \)，及 \( 2c=2 \) (正方形對角線?)。原解析利用橢圓定義：點 \( (c,1) \) 到兩焦點距離和 \( = \sqrt{(2c)^2+0} + \sqrt{0^2+1^2} = 2c + 1 = 2a \)，且 \( c=1 \) (因正方形邊長2，焦點水平距離2c=2? 需確認)。原答案：\( 1+\sqrt{5} \)。答案：\( 1+\sqrt{5} \) 報錯
ChatGPT DeepSeek
107學測數學考科-B
如右圖所示（只是示意圖），將梯子AB靠在與地面垂直的牆AC上，測得與水平地面的夾角∠ABC為60°。將在地面上的底B沿著地面向外拉51公分到點F（即FB=51公分），此時梯子EF與地面的夾角∠EFC之正弦值為\(\sin ∠EFC = 0.6\)，則梯子長 \( AB = \) __________ 公分。
答案
107學測數學考科-C
平面上兩點 \( A \)、\( B \) 之距離為5，以 \( A \) 為圓心作一半徑為 \( r \)（0 < \( r < 5 \)）的圓 \(\Gamma\)，過 \( B \) 作圓 \(\Gamma\) 的切線，切點（之一）為 \( P \)。當 \( r \) 變動時，\(\triangle PAB\) 的面積最大可能值為 __________。（化成最簡分數）
答案
107學測數學考科-H
將一塊邊長 \( AB = 15 \) 公分，\( BC = 20 \) 公分的長方形鐵片 \( ABCD \) 沿對角線 \( BD \) 對摺後豎立，使得平面 \( ABD \) 與平面 \( CBD \) 垂直，則 \( A \)、\( C \) 兩點（在空間）的距離 \( AC = \) __________ 公分。（化成最簡根式）
答案
108學測數學考科-C
某高中已有一個長90公尺，寬60公尺的足球練習場。若想要在足球練習場的外圍鋪設內圈總長度為400公尺的跑道，跑道規格為左右兩側各垂直徑相同的半圓，而中間是上下各一條的直線跑道，直線跑道與足球練習場的長邊平行（如示意圖），則圖中一條直線跑道 \(AB\) 長度的最大可能整數值為 __________ 公尺。
答案
110學測數學考科_03
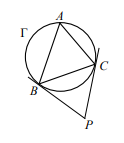如右圖，\(\triangle ABC\) 為銳角三角形，\( P \) 為 \(\triangle ABC\) 外接圓 \( \Gamma \) 外的一點，且 \( PB \) 與 \( PC \) 都與圓 \( \Gamma \) 相切。設 \(\angle BPC = \theta\)，試問 \( \cos A \) 的值為下列哪一個選項？
(1) \(\sin 2\theta\)
(2) \(\frac{\sin \theta}{2}\)
(3) \(\sin \frac{\theta}{2}\)
(4) \(\frac{\cos \theta}{2}\)
(5) \(\cos \frac{\theta}{2}\)
答案
連接圓心 O，則 \(\angle OBP = \angle OCP = 90^\circ\)，四邊形 OBPC 中，\(\angle BOC = 360^\circ - 90^\circ - 90^\circ - \theta = 180^\circ - \theta\)。圓周角 \(\angle A = \frac{1}{2} \angle BOC = 90^\circ - \frac{\theta}{2}\)，故 \(\cos A = \cos(90^\circ - \frac{\theta}{2}) = \sin \frac{\theta}{2}\)。(3) 報錯
ChatGPT DeepSeek
114分科測驗數學甲試卷-03
《幾何原本》云：「給定相異兩點可決定一條直線」。相異三點共線僅決定1條直線。坐標平面上，圓 \(\Gamma_1: x^2+y^2=4\) 與兩坐標軸交於4點、圓 \(\Gamma_2: x^2+y^2=2\) 與直線 \(x-y=0\) 交於2點、與直線 \(x+y=0\) 交於2點。試問這8點共可決定幾條不同的直線？
(1) 12
(2) 16
(3) 20
(4) 24
(5) 28
答案
114分科測驗數學甲試卷-11
坐標平面上有一平行四邊形 \( \Gamma \)，其中兩邊所在的直線與 \( 5x-y=0 \) 平行，另兩邊所在的直線與 \( 3x-2y=0 \) 垂直。令 \( \Gamma \) 的兩對角線交點為 \( Q \)。已知 \( \Gamma \) 有一頂點 \( P \)，滿足 \( \overrightarrow{PQ} = (10,-1) \)，則 \( \Gamma \) 的面積為為__________。
答案
204
設兩鄰邊向量：
\( \vec{u} \parallel 5x-y=0 \Rightarrow \vec{u} = b(1,5) \)
\( \vec{v} \perp 3x-2y=0 \Rightarrow \vec{v} = a(3,-2) \)
對角線向量和：\( \vec{u} + \vec{v} = 2\overrightarrow{PQ} = (20,-2) \)
解 \( (3a+b, -2a+5b) = (20,-2) \) 得 \( a=6, b=2 \)
面積 =\( |\begin{vmatrix}2&10 \\ 18&-12 \end{vmatrix}| = |2 \cdot (-12) - 10 \cdot 18| = |-24 - 180| = 204 \) 報錯
ChatGPT DeepSeek試題內容
試題內容
選擇(填)題答案
非選擇題評分原則
105指考數學甲試題-1)
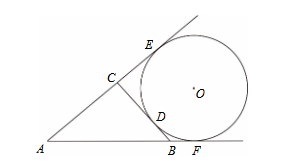
如圖，已知圓\(O\)與直線\(BC\)、直線\(AC\) 、直線\(AB\)均相切，且分別相切於\(D\)、\(E\)、\(F\)。又\(BC = 4\)，\(AC = 5\)，\(AB = 6\) 。假設\(\overline{BF}=x\)，試利用\(x\)分別表示\(\overline{BD}\)，\(\overline{CD}\)以及\(\overline{AE}\)，並求出\(x\)之值。(4分)
答案
根據圓的切線長定理，從圓外一點引圓的兩條切線，它們的切線長相等。
因為圓\(O\)與直線\(AB\)、\(BC\)相切，所以\(\overline{BF}=\overline{BD}=x\) 。
因為\(BC = 4\)，所以\(\overline{CD}=BC - \overline{BD}=4 - x\)。
又因為圓\(O\)與直線\(AC\)、\(AB\)相切，所以\(\overline{AE}=\overline{AF}\)。
而\(\overline{AF}=AB - \overline{BF}=6 - x\)，所以\(\overline{AE}=6 - x\)。
再根據\(\overline{AC}=\overline{AE}+\overline{CD}\)，即\(5=(6 - x)+(4 - x)\)。
解方程\(5 = 6 - x + 4 - x\)：
\[
\begin{align*}
5&=10 - 2x\\
2x&=10 - 5\\
2x&=5\\
x&=\frac{5}{2}
\end{align*}
\]
綜上，\(\overline{BD}=x=\frac{5}{2}\)，\(\overline{CD}=4 - x=\frac{3}{2}\)，\(\overline{AE}=6 - x=\frac{7}{2}\)，\(x\)的值為\(\frac{5}{2}\)。 報錯
ChatGPT DeepSeek
