質量720kg的無人駕駛實驗性電動車以20m/s等速度在斜面上前進。已知電動車以1200V的電池提供動力來源，且馬達的電能轉換作功的效率接近100%，在直線爬升過程中，除了須克服重力之外，仍須克服600N的空氣阻力，其他阻力則忽略不計。若電動車在斜面上前進120s，爬升的垂直高度為200m，則該電池必須提供約多少A的電流？（取重力加速度g=10m/s\(^2\)）
(A)5.0 (B)10 (C)15 (D)20 (E)25
答案
動能計算
114物理分科測驗14
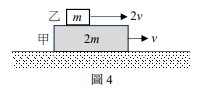
光滑水平面上有兩個質量不同的小木塊，其中一個為靜止，另一個速率為 \( v \)，兩木塊發生一維正面碰撞，碰撞後兩木塊的速度分別為 \( v_1 \) 與 \( v_2 \)。下列關於碰撞前後兩木塊速度的敘述哪些正確？
(A)無論是否為彈性碰撞，在碰撞後 \( v_1 \) 與 \( v_2 \) 皆不為零
(B)若為彈性碰撞，則碰撞後 \( v_1 \) 與 \( v_2 \) 皆不為零
(C)若為彈性碰撞，則 \( |v_1 – v_2| = v \)
(D)若為非彈性碰撞，則 \( |v_1 – v_2| \) 必不為零
(E)若為非彈性碰撞，則 \( |v_1 – v_2| \) 必大於 \( v \)
答案
114物理分科測驗15
如圖4所示，質量為2m之木塊甲放在光滑水平面上，其上置放質量為m之木塊乙，兩木塊間接觸面並非光滑。當時間t=0時，地面靜止觀察者測得木塊甲與乙的速度方向皆向右，量值分別為v與2v。若木塊乙沒有掉落，則下列欲述哪些正確？
(A)木塊甲的速率最大為 \( \frac{2v}{3} \) (B)木塊甲的速率最大為 \( \frac{4v}{3} \)
(C)木塊乙的速率最小為 \( \frac{2v}{3} \) (D)木塊乙的速率最小為 \( \frac{4v}{3} \)
(E)兩木塊之總動能因摩擦力而損失的最大值為 \( \frac{mv^2}{3} \)
答案
114物理分科測驗19
[題組:第19-20題]
◎某舊式腳踏車使用的「湯匙煞車」系統是在兩輪胎上方加上一個像湯匙的煞車片，如圖7所示。
煞車時，連桿會使煞車片施加一正向推力壓在輪胎表面上，因而產生摩擦力使車子減速。若煞車片所施的推力足夠大，則即使腳踏車在行進中，其車輪仍會被「鎖死」，也就是車輪完全不轉動而和地面處於動摩擦的狀態。
已知該腳踏車之兩輪胎和地面間的靜摩擦係數皆為 \( \mu_{st} = 0.80 \)，動摩擦係數皆為 \( \mu_{kt} = 0.50 \)；煞車片與兩輪胎間的靜摩擦係數皆為 \( \mu_{sb} = 0.60 \)，動摩擦係數皆為 \( \mu_{kb} = 0.40 \)。取重力加速度 \( g = 10 \, \text{m/s}^2 \)，並假設此腳踏車和騎車者的總質量為100kg，且車輪質量可忽略不計。
當腳踏車在水平地面上以4.0m/s等速度前進時，因緊急煞車以致兩車輪瞬間被鎖死，則此腳踏車在完全停止之前，最多還會再前進多少距離？（4分）
[題組題]
答案
114學測自然考科19
國際太空站（簡稱 ISS）主要用於進行微重力環境下的各種實驗，其繞行地球的週期為 90 分鐘，而任何質量的同步衛星，其繞行地球的週期和地球自轉的週期相同。已知沿圓形軌道繞行地球的物體，其動能 T 與重力位能 U 的關係為 \( 2T = -U \)。若 ISS 與某同步衛星的軌道皆近似圓形，則 ISS 與該同步衛星比較時，下列敘述哪些正確？（應選 2 項）
(A) ISS 的軌道半徑一定比較大
(B) ISS 的繞力學能一定比較大
(C) ISS 的重力位能一定比較大
(D) ISS 的速率一定比較大
(E) ISS 的加速度量值一定比較大
答案
105學測自然試題-22
氣候是長時間尺度下，地球系統中能量交換後呈現的現象。討論氣候變遷時的重點即是地球系統能量的收支平衡。下列有關能量平衡的敘述，何者正確？
(A)冬季時，高緯度溫度較低緯度寒冷，主要是因為距離太陽較遠，單位面積接收到的能量較少
(B)地球能量主要靠傳導散入外太空
(C)地表接收到的能量大於放出的能量時會造成平均溫度上升
(D)溫室氣體主要是透過吸收太陽輻射，而破壞地球能量的收支平衡
(E)地表吸收太陽光後會反射短波輻射
答案
105學測自然試題-30
將一個小球從地面鉛直上拋，假設空氣阻力可以忽略。圖 10 中甲時刻和乙時刻分別對應於小球往上升及往下掉的過程中，在任一相同高度處的運動狀態，則下列有關小球於甲、乙兩時刻對應的物理量，哪些一定相同？（應選 3 項）
(A)甲、乙兩時刻的加速度
(B)甲、乙兩時刻的速度
(C)甲、乙兩時刻的重力位能
(D)甲、乙兩時刻的動能
(E)從地面至甲時刻的時間與自最高點掉落至乙時刻的時間
答案
105學測自然試題-44
一質量可忽略的理想彈簧左端固定於牆上，其力常數為 k，如圖15所示。一質量為 m 的木塊，以初速率 v 向左滑行於水平面上，在正面擠壓彈簧後與彈簧保持接觸，直到被向右彈回，兩者分離。已知彈簧壓縮量為 x 時，其彈簧位能 U = ½kx²，而木塊與彈簧系統的力學能，定義為木塊動能與彈簧位能的總和。依據上述資料，回答下列44-45題。
若木塊與水平面間沒有摩擦力，則木塊與彈簧系統的力學能守恆。在沒有摩擦力的假設下，下列敘述哪些正確？（應選3項）
(A) 彈簧最大壓縮量 $x =\sqrt{\frac{m}{k}}v$
(B) 在壓縮過程中，木塊的動能守恆
(C) 木塊彈回右方起始位置時的速率為 $v$
(D) 木塊在剛開始壓縮彈簧時受力最大
(E) 彈簧被壓縮到最短時，木塊所受彈簧作用力最大
答案
109學測自然試題-02
王君搭乘熱氣球在廣闊無風的平原上空觀賞風景，熱氣球以等速度5.0 m/s 鉛直上升時，王君不小心使相機從離地高度為100 m 處離手而成為自由落體，若不計空氣阻力並取重力加速度為10 m/s\(^2\) ，則相機著地前瞬間的速度量值約為多少m/s ？
(A)55
(B)45
(C)35
(D)25
(E)15
答案
109學測自然試題-48
48-49為題組
如圖11所示，今有質量分別為\( m_{甲} \)與\( m_{乙} \)之甲、乙兩小球，其質量比值 \(\frac{m_{甲}}{m_{乙}} = \alpha < 1\)，將兩小球分別用長度為L的細線懸掛於同一固定點O，甲球靜止懸掛，而乙球向右拉直至細線呈現水平，然後靜止釋放乙球使其與甲球產生碰撞，且兩球立即黏在一起，黏在一起後濾起的最大高度為\( L/2 \)，圖12為其示意圖，細繩質量及空氣阻力均可忽略。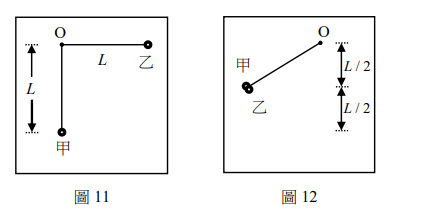
48. 假設以兩球自然下垂時的最低點為位能零點，則因碰撞而損失的力學能佔原來總力學能的比例為下列何者？
(A) \(\frac{1}{\alpha}\) (B) \(\frac{\alpha}{2}\) (C) \(\frac{1 – \alpha}{2}\) (D) \(\frac{1 + \alpha}{2}\) (E) 0
答案
乙球原高位能：( m_B g L )。碰撞前乙球速度v：( frac{1}{2} m_B v^2 = m_B g L ) → ( v = sqrt{2gL} )。完全非彈性碰撞後共同速度V：( m_B v = (m_A + m_B) V ) → ( V = frac{m_B}{m_A + m_B} v )。碰撞後上升高度h：( frac{1}{2} (m_A+m_B) V^2 = (m_A+m_B) g h ) → ( h = frac{V^2}{2g} = frac{m_B^2}{(m_A+m_B)^2} frac{v^2}{2g} = frac{m_B^2}{(m_A+m_B)^2} L )。已知h=L/2。故 ( frac{m_B^2}{(m_A+m_B)^2} = frac{1}{2} ) → ( frac{m_B}{m_A+m_B} = frac{1}{sqrt{2}} ) → ( m_A + m_B = sqrt{2} m_B ) → ( m_A = (sqrt{2}-1) m_B ) → ( alpha = m_A/m_B = sqrt{2}-1 )。原總力學能E_i = m_B g L。碰撞後瞬間動能E_k' = frac{1}{2} (m_A+m_B) V^2 = (m_A+m_B) g h = (m_A+m_B) g (L/2)。損失能量ΔE = E_i - E_k' = m_B g L - frac{(m_A+m_B)}{2} g L = g L [ m_B - frac{m_A+m_B}{2} ] = g L [ frac{2m_B - m_A - m_B}{2} ] = g L [ frac{m_B - m_A}{2} ]。損失比例 = ΔE / E_i = [ (m_B - m_A)/2 ] / m_B = frac{1}{2} (1 - alpha)。答案(C) (frac{1 - alpha}{2})。