平面幾何圖形
107學測數學考科-10
已知坐標平面上 \(\triangle ABC\)，其中 \(\overset{\rightharpoonup}{AB} = (-4,3)\)，且 \(\overset{\rightharpoonup}{AC} = \left( \frac{2}{5}, \frac{4}{5} \right)\)。試選出正確的選項。
(1) \(\overline{BC} = 5\)
(2) \(\triangle ABC\) 是直角三角形
(3) \(\triangle ABC\) 的面積為 \(\frac{11}{5}\)
(4) \(\sin B \gt \sin C\)
(5) \(\cos A \gt \cos B\)。
答案
(1) \( \overset{\rightharpoonup}{BC} = \overset{\rightharpoonup}{AC} - \overset{\rightharpoonup}{AB} = \left( \frac{22}{5}, -\frac{11}{5} \right) \)，長度 \( \frac{11\sqrt{5}}{5} \neq 5 \) ✗。
(2) \( \overline{AB}=5 \)，\( \overline{AC}=\frac{2\sqrt{5}}{5} \)，\( \overline{BC}=\frac{11\sqrt{5}}{5} \)，檢查得 \( \overline{AC}^2 + \overline{BC}^2 = \frac{4}{5} + \frac{121}{5} = 25 = \overline{AB}^2 \) ✓。
(3) 面積 \( \frac{1}{2} \times \frac{2\sqrt{5}}{5} \times \frac{11\sqrt{5}}{5} = \frac{11}{5} \) ✓。
(4) \( \sin B = \frac{\overline{AC}}{\overline{AB}} = \frac{2\sqrt{5}}{25} \)，\( \sin C = 1 \)，故 \( \sin B \lt \sin C \) ✗。
(5) \( \cos A = \frac{\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AC}}{5 \cdot \frac{2\sqrt{5}}{5}} = \frac{-8/5+12/5}{2\sqrt{5}} = \frac{4/5}{2\sqrt{5}} = \frac{2}{5\sqrt{5}} \)，\( \cos B = \frac{\overset{\rightharpoonup}{BA} \cdot \overset{\rightharpoonup}{BC}}{5 \cdot \frac{11\sqrt{5}}{5}} = \frac{ (4,-3) \cdot (22/5,-11/5) }{11\sqrt{5}} = \frac{88/5+33/5}{11\sqrt{5}} = \frac{121/5}{11\sqrt{5}} = \frac{11}{5\sqrt{5}} \)，故 \( \cos A \lt \cos B \) ✗。
故選(2)(3)。答案：(2)(3) 報錯
ChatGPT DeepSeek
108學測數學考科-01
108學測數學考科-10
在\(\triangle ABC\)中，已知\(50^\circ \lt \angle A \lt \angle B \lt 60^\circ\)，試選出正確的選項：
(1) \(\sin A \lt \sin B\) (2) \(\sin B \lt \sin C\) (3) \(\cos A \lt \cos B\) (4) \(\sin C \lt \cos C\) (5) \(\overline{AB} \lt \overline{BC}\)。
答案
由角度範圍知\(50^\circ \lt A \lt B \lt 60^\circ\)，則\(60^\circ \lt C \lt 80^\circ\)。
(1) 在\(0^\circ-90^\circ\)，角度大則正弦值大，故\(\sin A \lt \sin B\)。
(2) 同理\(\sin B \lt \sin C\)。
(3) 餘弦函數遞減，故\(\cos A \gt \cos B\)。
(4) \(C \gt 45^\circ\)，故\(\sin C \gt \cos C\)。
(5) 大角對大邊，\(\angle C \gt \angle A\)，故\(\overline{AB} \gt \overline{BC}\)。
故選(1)(2)。答案：(1)(2) 報錯
ChatGPT DeepSeek
108學測數學考科-E
如圖（此為示意圖），在\(\triangle ABC\)中，\(\overline{AD}\)交\(\overline{BC}\)於\(D\)點，\(\overline{BE}\)交\(\overline{AD}\)於\(E\)點，且\(\angle ACB = 30^\circ\)，\(\angle EDB = 60^\circ\)，\(\angle AEB = 120^\circ\)。若\(\overline{CD} = 15\)，\(\overline{ED} = 7\)，則\(\overline{AB} = \) __________。
答案
由角度關係可推\(\triangle BDE\)為正三角形，\(\overline{BE}=7\)；\(\triangle ACD\)中，\(\angle ACD=30^\circ\)，\(\angle ADC=120^\circ\)，推得\(\overline{AD}=15\)，故\(\overline{AE}=8\)。在\(\triangle ABE\)中，\(\angle AEB=120^\circ\)，由餘弦定理：\(\overline{AB}^2 = 8^2+7^2-2\cdot8\cdot7\cdot\cos120^\circ = 64+49+56=169\)，故\(\overline{AB}=13\)。答案：13 報錯
ChatGPT DeepSeek
109學測數學考科-07
坐標平面上，函數圖形 \(y = -\sqrt{3}x^3\) 上有兩點 \(P, Q\) 到原點距離皆為 1。已知點 \(P\) 坐標為 \((\cos\theta, \sin\theta)\)，試問點 \(Q\) 坐標為何？
(1) \((\cos(-\theta), \sin(-\theta))\)
(2) \((-\cos\theta, \sin\theta)\)
(3) \((\cos(-\theta), -\sin\theta)\)
(4) \((-\cos\theta, \sin(-\theta))\)
(5) \((\cos\theta, -\sin\theta)\)。
答案
109學測數學考科-13
如示意圖，四面體 \( OABC \) 中，\( \triangle OAB \) 和 \( \triangle OAC \) 均為正三角形，\( \angle BOC = 30^\circ \)。試選出正確的選項。
(1) \( BC \gt OC \)
(2) \( \triangle OBC \) 是等腰三角形
(3) \( \triangle OBC \) 的面積大於 \( \triangle OAB \) 的面積
(4) \( \angle CAB = 30^\circ \)
(5) 平面 \( OAB \) 和平面 \( OAC \) 的夾角（以銳角計）小於 \( 30^\circ \)。
答案
109學測數學考科-D
平面上有一等形 \(ABCD\)，其中 \(AB=BC=\sqrt{2}\)，\(\overline{AD}=\overline{CD}=2\)，\(\angle BAD=135^\circ\)。則 \(\overline{AC}=\) __________（化為最簡根式）
答案
110學測數學考科_03
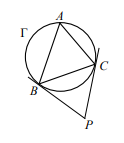如右圖，\(\triangle ABC\) 為銳角三角形，\( P \) 為 \(\triangle ABC\) 外接圓 \( \Gamma \) 外的一點，且 \( PB \) 與 \( PC \) 都與圓 \( \Gamma \) 相切。設 \(\angle BPC = \theta\)，試問 \( \cos A \) 的值為下列哪一個選項？
(1) \(\sin 2\theta\)
(2) \(\frac{\sin \theta}{2}\)
(3) \(\sin \frac{\theta}{2}\)
(4) \(\frac{\cos \theta}{2}\)
(5) \(\cos \frac{\theta}{2}\)
答案
連接圓心 O，則 \(\angle OBP = \angle OCP = 90^\circ\)，四邊形 OBPC 中，\(\angle BOC = 360^\circ - 90^\circ - 90^\circ - \theta = 180^\circ - \theta\)。圓周角 \(\angle A = \frac{1}{2} \angle BOC = 90^\circ - \frac{\theta}{2}\)，故 \(\cos A = \cos(90^\circ - \frac{\theta}{2}) = \sin \frac{\theta}{2}\)。(3) 報錯
ChatGPT DeepSeek
110學測數學考科_04
設 \( a \) 與 \( b \) 都是平面上不為零的向量。若 \( 2\overset{\rightharpoonup}{a} + \overset{\rightharpoonup}{b} \) 與 \( \overset{\rightharpoonup}{a} + 2\overset{\rightharpoonup}{b} \) 所張成的三角形面積為 \( 6 \)，則 \( 3\overset{\rightharpoonup}{a} + \overset{\rightharpoonup}{b} \) 與 \( \overset{\rightharpoonup}{a} + 3\overset{\rightharpoonup}{b} \) 所張成的三角形面積為下列哪一個選項？
(1) 8
(2) 9
(3) 12
(4) 13.5
(5) 16
答案
設 \( a, b \) 所張成的平行四邊形面積為 \( \Delta \)，則 \( 2a+b \) 與 \( a+2b \) 所張成的平行四邊形面積為 \( \begin{vmatrix} 2 & 1 \\ 1 & 2 \end{vmatrix} \Delta = 3\Delta \)，三角形面積為 \( \frac{1}{2} \times 3\Delta = 6 \)，得 \( \Delta = 4 \)。\( 3a+b \) 與 \( a+3b \) 所張成的平行四邊形面積為 \( \begin{vmatrix} 3 & 1 \\ 1 & 3 \end{vmatrix} \Delta = 8 \times 4 = 32 \)，三角形面積為 \( \frac{1}{2} \times 32 = 16 \)。(5) 報錯
ChatGPT DeepSeek
