庫侖定律

以等長細繩懸掛半徑均為 \( r \)、質量均為 \( m \) 的兩相同金屬小球於固定點 \( O \)，兩小球帶電量相同，因互斥分開，達到平衡後，球心相距 \( 2D (r \ll D) \)，如圖3所示。若固定點到球心連線的垂直距離為 \( L \)，庫侖常數為 \( k_e \)，重力加速度為 \( g \)，細繩質量可忽略，則每顆球上的電量約為下列何者？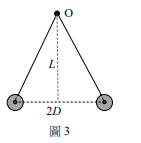
(A) \( 2\sqrt{\frac{mgD^3}{k_eL}} \)
(B) \( \sqrt{\frac{mgD^3}{k_eL}} \)
(C) \( \frac{1}{2}\sqrt{\frac{mgD^3}{k_eL}} \)
(D) \( 2\sqrt{\frac{k_eL}{mgD^3}} \)
(E) \( \sqrt{\frac{k_eL}{mgD^3}} \)

三個點電荷排列成一直線，若Q 為電量（Q ＞0），R 為點電荷間的距離，且所有電荷皆固定不動，則下列選項中，位於左端的電荷所受到靜電力的合力量值何者最大？