[題組:第24-26題]
在圖10中，若當光在水中傳遞10cm後，其強度至少仍有起始強度的0.37倍，則可能的波長範圍為何？即 \( \lambda_L \lt \lambda \lt \lambda_H \)，求 \( \lambda_L \)及\( \lambda_H \)。（須有說明或計算過程）（4分）
指數與對數
110學測數學考科_02
五項實數數列 \( a_1, a_2, a_3, a_4, a_5 \) 的每一項都大於1，且每相鄰的兩項中，都有一數是另一數的兩倍。若 \( a_1 = \log_{10} 36 \)，則 \( a_5 \) 有多少種可能的值？
(1) 3
(2) 4
(3) 5
(4) 7
(5) 8
答案
110學測數學考科_E
將 \((\sqrt[3]{49})^{100}\) 寫成科學記號 \((\sqrt[3]{49})^{100} = a \times 10^n\)，其中 \(1 \leq a < 10\)，且 \(n\) 為正整數。若 \(a\) 的整數部分為 \(m\)，則數對 \((m,n) = (\underline{\qquad\qquad}, \underline{\qquad\qquad})\)。
[選填題]
答案
111學測數學A考科-02
某品牌計算機在計算對數 \( \log_a b \) 時需按 \( \boxed{\log} \boxed{a} \boxed{b} \)。某生在計算 \( \log_a b \) 時（其中 \( a \gt 1 \) 且 \( b \gt 1 \)）順序弄錯，誤按 \( \boxed{\log} \boxed{b} \boxed{a} \)，所得為正確值的 \( \frac{9}{4} \) 倍。試選出 a，b 間的關係式。
(1) \( a^2 = b^3 \) (2) \( a^3 = b^2 \) (3) \( a^4 = b^9 \) (4) \( 2a = 3b \) (5) \( 3a = 2b \)
答案
111學測數學A考科-04
設等差數列 \( \langle a_n \rangle \) 之首項 \( a_1 \) 與公差 \( d \) 皆為正數，且 \( \log a_1 \cdot \log a_3 \cdot \log a_6 \) 依序也成等差數列。試選出數列 \( \log a_1 \cdot \log a_3 \cdot \log a_6 \) 的公差。
(1) \( \log d \) (2) \( \log \frac{2}{3} \) (3) \( \log \frac{3}{2} \) (4) \( \log 2d \) (5) \( \log 3d \)
答案
112學測數學A考科-03
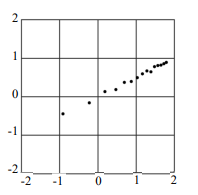某生推導出兩物理量 \( s \)，\( t \) 應滿足一等式。為了驗證其理論，他做了實驗得到15筆兩物理量的數據 \((s_k, t_k), k=1, \ldots, 15\) 。老師建議他將其中的 \( t_k \) 先取對數，在坐標平面上標出對應的點 \((s_k, \log t_k), k=1, \ldots, 15\) ，如右圖所示；其中第一個數據為橫軸坐標，第二個數據為縱軸坐標。利用迴歸直線分析，某生印證了其理論。
試問該生所得 \( s \)，\( t \) 的關係式最可能為下列哪一選項？
\[(1) \quad s = 2t \quad (2) \quad s = 3t \quad (3) \quad t = 10^5\]
\[(4) \quad t^2 = 10^5 \quad (5) \quad t^3 = 10^5\]
答案
113學測數學A考科_01
研究顯示：服用某藥物後，在使用者體內的藥物殘留量隨時間呈指數型衰退。已知在服用某藥物 2 小時後，體內仍殘留有該藥物的一半劑量，試問下列哪一選項正確？
(1)服用 3 小時後，體內仍殘留有該藥物的 \(\frac{1}{3}\) 劑量
(2)服用 4 小時後，體內仍殘留有該藥物的 \(\frac{1}{4}\) 劑量
(3)服用 6 小時後，體內仍殘留有該藥物的 \(\frac{1}{6}\) 劑量
(4)服用 8 小時後，體內仍殘留有該藥物的 \(\frac{1}{8}\) 劑量
(5)服用 10 小時後，體內仍殘留有該藥物的 \(\frac{1}{10}\) 劑量
答案
113學測數學A考科_07
今坐標平面上滿足 \(y = \log x\) 的點 \((x, y)\) 所成圖形為 \(\Gamma\)，試問滿足下列哪些關係式的 \((x, y)\) 所成圖形與 \(\Gamma\) 完全相同？
(1) \(y + \frac{1}{2} = \log (5x)\)
(2) \(2y = \log (x^2)\)
(3) \(3y = \log (x^3)\)
(4) \(x = 10^y\)
(5) \(x^3 = 10^{(y^3)}\)
答案
107指考數學乙試題-03
設 \( a \lt b \lt 2^{10} \)，其中 \(\log a = 3\)。已知利用 \(\log a 、 \log(2^{10})\) 的值與內插法求得 \(\log b\) 的近似值為 3.0025，試問 \(b\) 的值最接近下列哪一個選項？（註：\(\log 2 \approx 0.3010\)）
(1) 1002 (2) 1006 (3) 1010 (4) 1014 (5) 1018
答案
\(\log a = 3 \Rightarrow a = 10^3 = 1000\)，\(\log(2^{10}) = 10\log 2 \approx 3.010\)。
已知 \(\log b \approx 3.0025\)，所以 \(b \approx 10^{3.0025} = 10^3 \times 10^{0.0025} \approx 1000 \times (1 + 0.0025\ln 10)\)。
\(\ln 10 \approx 2.302585\)，所以 \(10^{0.0025} \approx 1 + 0.0025 \times 2.302585 \approx 1.005756\)。
\(b \approx 1000 \times 1.005756 \approx 1005.756\)，最接近 1006。
答案為 (2)。 報錯
ChatGPT DeepSeek
107指考數學乙試題-05
設 \(2^x = 3\)，\(3^y = 4\)。試選出正確的選項。（註：\(\log 2 \approx 0.3010\)，\(\log 3 \approx 0.4771\)）
(1) \(x \lt 2\) (2) \(y \gt \frac{3}{2}\) (3) \(x \lt y\) (4) \(xy = 2\) (5) \(x + y \lt 2\sqrt{2}\)
答案
\(x = \log_2 3 = \frac{\log 3}{\log 2} \approx \frac{0.4771}{0.3010} \approx 1.585 \< 2\)，(1)正確。
\(y = \log_3 4 = \frac{\log 4}{\log 3} \approx \frac{0.6021}{0.4771} \approx 1.262 \< 1.5\)，(2)錯誤。
\(x \approx 1.585 \gt y \approx 1.262\)，(3)錯誤。
\(xy = \log_2 3 \times \log_3 4 = \log_2 4 = 2\)，(4)正確。
\(x+y \approx 2.847\)，\(2\sqrt{2} \approx 2.828\)，\(x+y \gt 2\sqrt{2}\)，(5)錯誤。
答案為 (1)(4)。 報錯
ChatGPT DeepSeek
