家政老師要將甲、乙、丙、丁、戊、己、庚、辛等8位學生平均分為4組，每組2人進行料理比賽，基於秩序考量，甲同學不可以跟乙同學同組，且乙同學也不可以跟丙同學同組，還有丙同學也不可以跟丁同學同組，請問老師有多少种分组方法？
\((1) 54\)種
\((2) 63\)種
\((3) 76\)種
\((4) 82\)種
\((5) 95\)種
8人平均分4組總方法：\(\frac{C_8^2C_6^2C_4^2C_2^2}{4!} = 105\)。用容斥原理減去違規組合：甲與乙同組、乙與丙同組、丙與丁同組的方法各 \(\frac{C_6^2C_4^2C_2^2}{3!} = 15\)，加回重減部分，得 \(105 - 3\times15 + 3 = 63\)。答案：\((2)\)
[題組:第18到20題]王先生參加一個4天3夜的渡假活動，旅行社提供3間不同的單人小木屋 \(A\)、\(B\)、\(C\) 供住宿，參加旅客必須每天在不同的小木屋留宿。例如：王先生「第1天住 \(A\) 房、第2天住 \(B\) 房、第3天住 \(C\) 房」與「第1天住 \(A\) 房、第2天住 \(C\) 房、第3天住 \(B\) 房」視為不同的安排。試問王先生這3夜住宿順序的安排方式有幾種？
\((1) 3\)種
\((2) 4\)種
\((3) 6\)種
\((4) 9\)種
\((5) 12\)種
[題組:第18到20題]王先生參加一個4天3夜的渡假活動，旅行社提供3間不同的單人小木屋 \(A\)、\(B\)、\(C\) 供住宿，參加旅客必須每天在不同的小木屋留宿。若王先生這3夜的住宿安排順序為「第1天住 \(A\) 房、第2天住 \(B\) 房、第3天住 \(C\) 房」，好朋友丁小姐和呂先生也對該行程有興趣，但兩人不得選擇王先生已選定的小木屋留宿，每人每晚均在不同的小木屋住宿，且每間小木屋每晚只能供1人住宿。則丁小姐和呂先生這3夜的住宿順序有幾種安排的方式？
[題組題][題組:第18到20題]王先生參加一個4天3夜的渡假活動，旅行社提供4間不同的單人小木屋 \(D\)、\(E\)、\(F\)、\(G\) 供住宿，參加旅客必須每天在不同的小木屋留宿。結束旅程後，3人對此行程非常滿意，決定再次參加此4天3夜的渡假活動。若此次旅行社共安排4間不同的單人小木屋 \(D\)、\(E\)、\(F\)、\(G\) 供3人住宿，每人每晚均在不同的小木屋住宿，且每間小木屋每晚只能供1人住宿。此次3人一起進行3夜的住宿規劃，則3人的3夜住宿順序有幾種安排的方式？
[題組題]先安排王先生：從4間選3間排列，\(P_4^3 = 24\) 種。再安排丁小姐，分兩類：第1天住王先生選過的房（2種）或未選的房（1種），共3種，對應呂先生各4種。總方法 \(24\times3\times4 = 1056\) 種。答案：\(1056\)種
三角形 \(ABC\) 是一個邊長為 3 的正三角形,如下圖所示。若在每一邊的兩個三等分點中,各選取一點連成三角形,則下列哪些選項是正確的？
(1) 依此方法可能連成的三角形一共有 8 個
(2) 這些可能連成的三角形中,恰有 2 個是銳角三角形
(3) 這些可能連成的三角形中,恰有 3 個是直角三角形
(4) 這些可能連成的三角形中,恰有 3 個是鈍角三角形
(5) 這些可能連成的三角形中,恰有 1 個是正三角形
\[
\boxed{\text{步驟一：計算三角形總數}}
\]
\[
\begin{aligned}
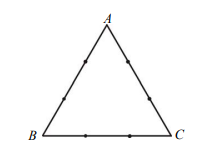
\text{每邊三等分點數：} & 2 \text{ 個（不包含端點）} \\
\text{選擇方式：} & \text{從三邊各選一點} \\
\text{總數：} & 2 \times 2 \times 2 = 8
\end{aligned}
\]
\[
\boxed{\text{步驟二：分類三角形類型}}
\]
\[
\begin{array}{|c|c|}
\hline
\text{類型} & \text{對應三角形} \\
\hline
\text{正三角形（銳角）} & \triangle A_1A_5A_3,\ \triangle A_2A_4A_6 \\
\hline
\text{直角三角形} & \triangle A_1A_6A_3,\ \triangle A_2A_3A_5,\ \triangle A_1A_5A_4 \\
& \triangle A_1A_6A_4,\ \triangle A_2A_6A_3,\ \triangle A_2A_4A_5 \\
\hline
\text{鈍角三角形} & \text{無} \\
\hline
\end{array}
\]
\[
\boxed{\text{步驟三：判斷選項}}
\]
\[
\begin{aligned}
& \text{(1) 8個三角形：} \checkmark \\
& \text{(2) 包含正三角形：} \checkmark \\
& \text{(3) 包含等腰直角三角形：} \times \\
& \text{(4) 直角三角形恰有6個：} \checkmark \text{（但題目可能問其他）} \\
& \text{(5) 鈍角三角形存在：} \times \\
\\
& \therefore \text{正確答案：} (1)(2)
\end{aligned}
\]
將 24 顆雞蛋分裝到紅、黃、綠的三個籃子。每個籃子都要有雞蛋,且黃、綠兩個籃子裡都裝奇數顆。請選出分裝的方法數。
(1) 55
(2) 66
(3) 132
(4) 198
(5) 253
一個房間的地面是由 12 個正方形所組成,如右圖。
今想用長方形瓷磚舖滿地面,已知每一塊長方形瓷磚可以覆蓋兩個相鄰的正方形,即
或
。則用 6 塊瓷磚舖滿房間地面的方法有 \(~~~~~~~~~~~\) 種。
[選填]原圖形由兩個 \(2 \times 3\) 矩形組成。分兩類討論如下：
---
**① 排出兩個 \(2 \times 3\) 矩形：**
在 \(4 \times 3\) 方格中，排出一個 \(2 \times 3\) 矩形有 \(3\) 種方法；
對每種排法，在剩下的區域排出另一個 \(2 \times 3\) 矩形也有 \(3\) 種方法。
由乘法原理得：
\[
3 \times 3 = 9 \text{ 種}。
\]
---
**② 沒有排出 \(2 \times 3\) 矩形：**
此類排法根據圖示（未附）共有 \(2\) 種方法。
---
總方法數為：
\[
9 + 2 = 11 \text{ 種}。
\]
小燦預定在陽台上種植玫瑰、百合、菊花和向日葵等四種盆栽。如果陽台上的空間最多能種 8 盆,可以不必擺滿,並且每種花至少一盆,則小燦買盆栽的方法共有 \(\boxed{~~~~~~~~~~}\) 種。
[選填]設玫瑰買 \(x\) 盆，百合 \(y\) 盆，菊花 \(z\) 盆，向日葵 \(t\) 盆
由題意可得
\[
x + y + z + t \leq 8 , \quad x, y, z, t \geq 1
\]
令
\[
x' = x-1,\quad y' = y-1,\quad z' = z-1,\quad t' = t-1
\]
則
\[
x', y', z', t' \geq 0 , \quad x' + y' + z' + t' \leq 4
\]
再引入輔助變數 \(w \geq 0\)，使
\[
x' + y' + z' + t' + w = 4
\]
此為非負整數解之個數問題，共有
\[
H_{5}^{4} = C_{4+5-1}^{4} = C_{8}^{4} = \frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1} = 70 \text{ 種}
\]
**答案：70 種**
小明想要安排從星期一到星期五共五天的午餐計畫。他的餐點共有四種選擇：牛肉麵、大油麵、咖喱飯及排骨飯。小明想要依據下列兩原則來安排他的午餐：
(甲)每天只選一種餐點但這五天中每一種餐點至少各點一次
(乙)連續兩天的餐點不能重複且不連續兩天吃麵食
根據上述原則，小明這五天共有幾種不同的午餐計畫？
(1) 52
(2) 60
(3) 68
(4) 76
(5) 84。
某班級50位學生，段考圓文、英文、數學及格的人數分別為45、39、34人，且英文及格的學生圓文也都及格。現假設數學和英文皆及格的有x人，數學及格但英文不及格的有y人。請選出正確的選項。
(1) \( x+y=39 \)
(2) \( y\leq11 \)
(3) 三種中至少有一科不及格的學生有39-x+y人
(4) 三種中至少有一科不及格的學生最少有11人
(5) 三種中至少有一科不及格的學生最多有27人。
