已知實係數多項式 \( f(x) \) 除以 \( x^2 – 14x + 13 \) 的餘式為 \( ax + b \),且 \( f(x) \) 除以 \( x – 1 \) 的餘式為4,則 \( a + b \) 的值為何?
(1) -1
(2) 0
(3) 1
(4) 4
(5) 13
方程求解
107指考數學乙試題-非選擇一(3)
(3) 若方程式 \( f(x) = 0 \) 有相異實根,試證兩根之積小於 4。
[非選擇題]設 \( f(x) = a(x+2)^2 + b \),且 \( f(x) = 0 \) 有兩相異實根 \( \alpha, \beta \)。
由 \( a(x+2)^2 + b = 0 \Rightarrow a(x^2 + 4x + 4) + b = 0 \Rightarrow ax^2 + 4a x + (4a+b) = 0 \)。
根與係數:\( \alpha\beta = \frac{4a+b}{a} = 4 + \frac{b}{a} \)。
由 (2) 知 \( \frac{b}{a} \lt 0 \),所以 \( \alpha\beta \lt 4 \)。
得證。
105指考數學乙試題-04
設\(f(x)\)為一未知的實係數多項式,但知道\(f(x)\)除以\((x-5)(x-6)^2\)的餘式為\(5x^2+6x+7\)。根據上述所給條件,請選出正確的選項。
(1) 可求出\(f(0)\)之值
(2) 可求出\(f(1)\)之值
(3) 可求出\(f(x)\)除以\((x-5)^2\)的餘式
(4) 可求出\(f(x)\)除以\((x-6)^2\)的餘式
(5) 可求出\(f(x)\)除以\((x-5)(x-6)\)的餘式
106指考數學乙試題-01
設 \( f(x) = x^3 + ax^2 + bx + c \) 為實係數多項式函數。若 \( f(1) = f(2) = 0 \) 且 \( f(3) = 4 \),則 \( a + 2b + c \) 的值是下列哪一個選項?
(1) 1
(2) 2
(3) 3
(4) 4
(5) 5
109指考數學乙(補考)試題-_A
若 \( f(x) \) 為二次的實係數多項式函數,且滿足 \( f(0)+f(1)=5 \),\( f(1)+f(2)=17 \),\( f(2)+f(0)=14 \),則 \( f(x)=\underline{\quad }x^2+\underline{\quad }x+9 \)
[選填題]\begin{align*}
&設 \ f(x) = ax^2 + bx + c,則: \\
&f(0) = c,\quad f(1) = a + b + c,\quad f(2) = 4a + 2b + c \\
\\
&將題目的條件代入,得聯立方程組: \\
&\begin{cases}
a + b + 2c = 5 \\
5a + 3b + 2c = 17 \\
4a + b + 2c = 14
\end{cases} \\
\\
&解此方程組,得 \ a = 3,\ b = 0,\ c = 1,故 \ f(x) = 3x^2 + 1。
\end{align*}
109指考數學乙(補考)-非選擇二(1)
二. 等比數列 \( \langle a_n \rangle \) 的前三項可表為 \(\begin{cases} a_1 = x^2 + x + 3 \\ a_2 = 2x + 2 \\ a_3 = x + 2 \end{cases}\),其中 \( x \) 為實數。試回答下列問題。
(1) 試求 \( x \) 的所有可能值。
$\begin{align*}
&(1) \ 因為\{a_n\}是等比數列,故\frac{a_2}{a_1}=\frac{a_3}{a_2},代入得: \\
&\frac{2x+2}{x^2+x+3}=\frac{x+2}{2x+2} \implies (x+2)(x^2+x+3)=(2x+2)^2 \\
&\implies x^3 + 3x^2 + 5x + 6 = 4x^2 + 8x + 4 \implies x^3 - x^2 - 3x + 2 = 0 \\
\\
&用牛頓有理根檢驗法,可能有理根為\pm1,\pm2,代入得x=2是根,因式分解為: \\
&(x-2)(x^2+x-1)=0 \implies 解為 \ x=2,\ \frac{-1\pm\sqrt{5}}{2}
\end{align*}$
108指考數學乙試題-稿B
已知實係數多項式 \( f(x) \) 除以 \( x^2 + 2 \) 的餘式為 \( x + 1 \)。若 \( xf(x) \) 除以 \( x^2 + 2 \) 的餘式為 \( ax + b \),則數對 \((a, b) = ( \underline{\qquad} , \underline{\qquad} )\)。
[選填題]105指考數學甲試題-01
請問下列選項中哪一個數值 \(a\) 會使得 \(x\) 的方程式 \(\log a-\log x=\log (a – x)\) 有兩相異實數解?
(1)\(a = 1\)
(2)\(a = 2\)
(3)\(a = 3\)
(4)\(a = 4\)
(5)\(a = 5\)
由\(\log a-\log x=\log (a - x)\),根據對數運算法則可得\(\log\frac{a}{x}=\log (a - x)\),則\(\frac{a}{x}=a - x\)(\(x\gt0\),\(a - x\gt0\)),整理得\(x^{2}-ax + a = 0\)。
此方程有兩相異實數解,則判別式\(\Delta = a^{2}-4a\gt0\),解得\(a\lt0\)或\(a\gt4\)。
又因為\(x\gt0\),\(a - x\gt0\),即\(x\lt a\),且\(x\)是\(x^{2}-ax + a = 0\)的根,由韋達定理\(x_1 + x_2 = a\),\(x_1x_2 = a\),所以\(a\gt0\)。
綜上,\(a\gt4\),只有\(a = 5\)滿足條件。
答案為(5)。
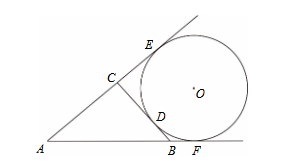
105指考數學甲試題-非選擇一(1)
如圖,已知圓\(O\)與直線\(BC\)、直線\(AC\) 、直線\(AB\)均相切,且分別相切於\(D\)、\(E\)、\(F\)。又\(BC = 4\),\(AC = 5\),\(AB = 6\) 。假設\(\overline{BF}=x\),試利用\(x\)分別表示\(\overline{BD}\),\(\overline{CD}\)以及\(\overline{AE}\),並求出\(x\)之值。(4分)
[非選擇題]106指考數學甲試題-03
試問在\(0\leq x\leq2\pi\)的範圍中,\(y = 3\sin x\)的函數圖形與\(y = 2\sin2x\)的函數圖形有幾個交點?
(1)2個交點
(2)3個交點
(3)4個交點
(4)5個交點
(5)6個交點
由\(3\sin x = 2\sin2x\),根據二倍角公式\(\sin2x = 2\sin x\cos x\),可得\(3\sin x = 2\times2\sin x\cos x\)。
移項得\(3\sin x - 4\sin x\cos x = 0\),提取公因式\(\sin x\)得\(\sin x(3 - 4\cos x)=0\) 。
則\(\sin x = 0\)或\(3 - 4\cos x = 0\)。
當\(\sin x = 0\)時,\(x = 0,\pi,2\pi\);
當\(3 - 4\cos x = 0\)時,\(\cos x=\frac{3}{4}\),在\(0\leq x\leq2\pi\)範圍內,\(x = 2k\pi\pm\arccos\frac{3}{4}\),\(k\in Z\),此時有兩個解(\(k = 0\)時的兩個值)。
所以共有\(5\)個交點。
答案為(4)。