在邊長為 13 的正三角形 \(ABC\) 上各邊分別取一點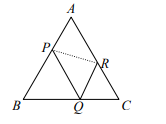 \(P, Q, R\),使得 \(APQR\) 形成一平行四邊形,如下圖所示:若平行四邊形 \(APQR\) 的面積為 \(20\sqrt{3}\),則線段 \(PR\) 的長度為 __________。
\(P, Q, R\),使得 \(APQR\) 形成一平行四邊形,如下圖所示:若平行四邊形 \(APQR\) 的面積為 \(20\sqrt{3}\),則線段 \(PR\) 的長度為 __________。
[選填]
\[
\begin{aligned}
&\text{四邊形 } APQR \text{ 為平行四邊形} \\
&\Rightarrow \frac{AP}{AB} = \frac{CQ}{CB} = \frac{CR}{AC} \\
&\Rightarrow AP = CR \quad (\because AB = AC) \\
\\
&\text{設 } AP = CR = x,\quad AR = 13 - x \\
\\
&\text{平行四邊形面積:} \\
&x(13 - x) \sin 60^\circ = 20\sqrt{3} \\
&\Rightarrow \frac{\sqrt{3}}{2} x(13 - x) = 20\sqrt{3} \\
&\Rightarrow x^2 - 13x + 40 = 0 \\
&\Rightarrow x = 5 \text{ 或 } 8 \\
\\
&\text{取 } AP=5,\ AR=8 \ (\text{或反之}),\text{餘弦定理求 } PR: \\
&PR = \sqrt{AP^2 + AR^2 - 2 \cdot AP \cdot AR \cdot \cos 60^\circ} \\
&\quad = \sqrt{25 + 64 - 2 \times 5 \times 8 \times \frac{1}{2}} \\
&\quad = \sqrt{89 - 40} = \sqrt{49} = 7
\end{aligned}
\]