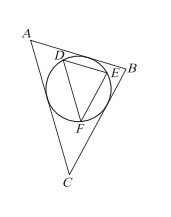
已知三角形 \(ABC\) 中:
\[
\angle A = 91^\circ, \quad \angle C = 29^\circ, \quad \angle B = 60^\circ
\]
(因為 \(180^\circ - 91^\circ - 29^\circ = 60^\circ\))
邊長:
\[
BC = a, \quad CA = b, \quad AB = c
\]
(即 \(a\) 對 \(\angle A\),\(b\) 對 \(\angle B\),\(c\) 對 \(\angle C\))
---
**(1) \( a^2 > b^2 + c^2 \)**
由餘弦定理:
\[
a^2 = b^2 + c^2 - 2bc\cos A
\]
\(\cos 91^\circ < 0\),所以 \(-2bc\cos A > 0\),因此
\[
a^2 > b^2 + c^2
\]
✅ 正確。
---
**(2) \( \frac{c}{a} > \sin 29^\circ \)**
正弦定理:
\[
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R
\]
所以
\[
\frac{c}{a} = \frac{\sin C}{\sin A} = \frac{\sin 29^\circ}{\sin 91^\circ}
\]
\(\sin 91^\circ \approx \sin 90^\circ = 1\),實際略大於 1(\(\sin 91^\circ \approx 0.99985\)),所以
\[
\frac{c}{a} \approx 0.99985^{-1} \times \sin 29^\circ \approx 1.00015 \times 0.4848 \approx 0.48487
\]
而 \(\sin 29^\circ \approx 0.4848\),比較:
\[
\frac{c}{a} \approx 0.48487 > 0.4848
\]
✅ 正確(雖然很接近,但確實大於)。
---
**(3) \( \frac{b}{a} > \cos 29^\circ \)**
\[
\frac{b}{a} = \frac{\sin B}{\sin A} = \frac{\sin 60^\circ}{\sin 91^\circ} \approx \frac{0.866025}{0.99985} \approx 0.86615
\]
\(\cos 29^\circ \approx 0.87462\),比較:
\[
0.86615 < 0.87462
\]
❌ 錯誤。
---
**(4) \( \frac{a^2 + b^2 - c^2}{ab} < \sqrt{3} \)**
由餘弦定理:
\[
\cos C = \frac{a^2 + b^2 - c^2}{2ab}
\]
所以
\[
\frac{a^2 + b^2 - c^2}{ab} = 2\cos C = 2\cos 29^\circ \approx 2 \times 0.87462 \approx 1.74924
\]
\(\sqrt{3} \approx 1.732\),比較:
\[
1.74924 > 1.732
\]
❌ 錯誤。
---
**(5) 外接圓半徑小於 \(c\)**
外接圓半徑 \(R = \frac{a}{2\sin A} \approx \frac{a}{2 \times 0.99985} \approx 0.500075 \times a\)
由正弦定理:
\[
c = 2R \sin C \implies R = \frac{c}{2\sin C} = \frac{c}{2 \times 0.4848} \approx \frac{c}{0.9696} \approx 1.0314 \times c
\]
等等,這裡要小心:題目給的 \(a,b,c\) 是邊長,\(R\) 是固定值。
用 \(a = 2R\sin A\),\(c = 2R\sin C\)。
比較 \(R\) 與 \(c\):
\[
c = 2R\sin C \implies \frac{R}{c} = \frac{1}{2\sin C} \approx \frac{1}{0.9696} \approx 1.0314
\]
所以 \(R \approx 1.0314 \times c > c\),因此 \(R < c\) 不成立。
❌ 錯誤。
---
**正確選項:** (1)、(2)
\[
\boxed{12}
\]
試題內容
試題內容
答題卷
選擇(填)題答案