〈無窮等比級數〉彙整頁面

101學測數學考科-14

若首項為 $a$,公比為 0.01 的無窮等比級數和等於循環小數$ 1.\overline{2}$,則 $a = \boxed{~~~~~~~~~~}$。

答案

無窮等比級數和公式為 $S = \frac{a}{1 - r}$,其中 $r = 0.01$。因此,$1.2 = \frac{a}{1 - 0.01} = \frac{a}{0.99}$,解得 $a = 1.2 \times 0.99 = 1.188$。因此,$a = \boxed{1.212}$。報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–08

設m, n為小於或等於4的相異正整數且a, b為非零實數。已知函數$f(x) = ax^m$與函數$g(x) = bx^n$的圖形恰有3個相異交點，請選出可能的選項。
(1) m, n皆為偶數且a, b同號
(2) m, n皆為偶數且a, b異號
(3) m, n皆為奇數且a, b同號
(4) m, n皆為奇數且a, b異號
(5) m, n為一奇一偶。

答案

解 $ax^m = bx^n \Rightarrow x^n (ax^{m-n} - b) = 0$。需恰有3個相異實根。
(1) m, n偶，a, b同號：$x=0$（重根），$x=\pm \sqrt[m-n]{\frac{b}{a}}$，共3個相異實根。
(2) m, n偶，a, b異號：$x=0$，另兩根為虛數，僅1實根。
(3) m, n奇，a, b同號：$x=0$，$x=\pm \sqrt[m-n]{\frac{b}{a}}$，共3個相異實根。
(4) m, n奇，a, b異號：$x=0$，另兩根為虛數，僅1實根。
(5) m, n一奇一偶：例如m=4, n=3，得 $x^3(x - \frac{b}{a})=0$，僅2個相異實根。
故選(1)(3)。答案：(1)(3) 報錯
 ChatGPT DeepSeek

加最愛

110學測數學考科_02

五項實數數列 $ a_1, a_2, a_3, a_4, a_5 $ 的每一項都大於1，且每相鄰的兩項中，都有一數是另一數的兩倍。若 $ a_1 = \log_{10} 36 $，則 $ a_5 $ 有多少種可能的值？
(1) 3
(2) 4
(3) 5
(4) 7
(5) 8

答案

設從 $ a_1 $ 到 $ a_5 $ 共經過「×2」x 次，「÷2」y 次，則 $ x+y=4 $。又 $ a_5 = \log_{10} 36 \times 2^{x-y} \gt 1 $，可得 $ x \ge y $。滿足 $ x+y=4 $ 且 $ x \ge y $ 的非負整數解有 (4,0), (3,1), (2,2) 共三組，故 $ a_5 $ 有 3 種可能值。(1) 報錯
 ChatGPT DeepSeek

加最愛

114學測數學A考科_07

已知數列 $\langle a_n \rangle$ 滿足 $3a_{n+1} = a_n + n$ (對任意正整數 $n$ 都成立) 且 $a_1 = 2$。令數列 $\langle b_n \rangle$ 滿足 $b_n = a_n – \frac{n}{2} + \frac{3}{4}$。試選出正確的選項。
(1) $a_2 = 2$
(2) $b_2 = \frac{3}{4}$
(3) 數列 $\langle b_n \rangle$ 是公比為 $\frac{2}{3}$ 的等比數列
(4) 對於任意正整數 $n$，$3^n a_n$ 皆為正整數
(5) $b_{10} \lt 10^{-4}$

答案

(1) ✗：$a_2=1$；(2) ✓：$b_2=\frac{3}{4}$；(3) ✗：公比為 $\frac{1}{3}$；
(4) ✓：令 $c_n=3^n a_n$，可得 $c_n$ 為正整數；(5) ✗：$b_{10}=\frac{1}{8748} \gt 10^{-4}$。
故選(2)(4)。報錯
 ChatGPT DeepSeek

加最愛

113學測數學A考科_01

研究顯示：服用某藥物後，在使用者體內的藥物殘留量隨時間呈指數型衰退。已知在服用某藥物 2 小時後，體內仍殘留有該藥物的一半劑量，試問下列哪一選項正確？
(1)服用 3 小時後，體內仍殘留有該藥物的 $\frac{1}{3}$ 劑量
(2)服用 4 小時後，體內仍殘留有該藥物的 $\frac{1}{4}$ 劑量
(3)服用 6 小時後，體內仍殘留有該藥物的 $\frac{1}{6}$ 劑量
(4)服用 8 小時後，體內仍殘留有該藥物的 $\frac{1}{8}$ 劑量
(5)服用 10 小時後，體內仍殘留有該藥物的 $\frac{1}{10}$ 劑量

答案

設初始劑量為 $A$，則殘留量函數為 $f(x) = A \cdot \left( \frac{1}{2} \right)^{\frac{x}{2}}$。
計算得 $f(4) = A \cdot \left( \frac{1}{2} \right)^2 = \frac{1}{4}A$，故選(2)。報錯
 ChatGPT DeepSeek

加最愛

113學測數學A考科_07

今坐標平面上滿足 $y = \log x$ 的點 $(x, y)$ 所成圖形為 $\Gamma$，試問滿足下列哪些關係式的 $(x, y)$ 所成圖形與 $\Gamma$ 完全相同？
(1) $y + \frac{1}{2} = \log (5x)$
(2) $2y = \log (x^2)$
(3) $3y = \log (x^3)$
(4) $x = 10^y$
(5) $x^3 = 10^{(y^3)}$

答案

(1) 圖形平移，不全等；(2) 定義域包含負 $x$，不全等；(3) 等價於 $y=\log x$；(4) 等價於 $y=\log x$；(5) 不滿足一對一關係。
故選(3)(4)。報錯
 ChatGPT DeepSeek

加最愛

107指考數學乙試題-04

已知数列 $\langle a_n \rangle, \langle b_n \rangle, \langle c_n \rangle, \langle d_n \rangle, \langle e_n \rangle$ 定義如下：
\[a_n = (-1)^n ; \quad b_n = a_n + a_{n+1} ; \quad c_n = \left( -\frac{\sqrt{10}}{3} \right)^n ; \quad d_n = \frac{1}{3} c_n ; \quad e_n = \frac{1}{c_n} ; \quad 其中 n = 1, 2, 3, \ldots\]
下列選項中，試選出會收斂的無窮級數。
(1) $ \sum_{n=1}^{\infty} a_n $
(2) $ \sum_{n=1}^{\infty} b_n $
(3) $ \sum_{n=1}^{\infty} c_n $
(4) $ \sum_{n=1}^{\infty} d_n $
(5) $ \sum_{n=1}^{\infty} e_n $

答案

(1) $a_n$ 震盪，級數發散。
(2) $b_n = (-1)^n + (-1)^{n+1} = 0$，級數收斂到 0。
(3) $c_n$，公比 $r = -\frac{\sqrt{10}}{3}$，$|r| \approx 1.054 \gt 1$，發散。
(4) $d_n$，公比同 (3)，發散。
(5) $e_n = \left( -\frac{3}{\sqrt{10}} \right)^n$，公比絕對值約 0.948 \< 1，收斂。
答案為 (2)(5)。報錯
 ChatGPT DeepSeek

加最愛

106指考數學乙試題-05

設 $ a_1, a_2, \cdots, a_n, \cdots $ 是一公比為 $\frac{1}{2}$ 的無窮等比數列且 $a_1 = 1$。試問以下哪些數列會收斂？
(1) $-a_1, -a_2, \cdots, -a_n, \cdots$
(2) $a_1^2, a_2^2, \cdots, a_n^2, \cdots$
(3) $\sqrt{a_1}, \sqrt{a_2}, \cdots, \sqrt{a_n}, \cdots$
(4) $\frac{1}{a_1}, \frac{1}{a_2}, \cdots, \frac{1}{a_n}, \cdots$
(5) $\log a_1, \log a_2, \cdots, \log a_n, \cdots$

答案

$ a_n = (1/2)^{n-1} $。
(1) $ -a_n $ 仍收斂到 0，正確。
(2) $ a_n^2 = (1/4)^{n-1} $ 收斂到 0，正確。
(3) $ \sqrt{a_n} = (1/\sqrt{2})^{n-1} $ 收斂到 0，正確。
(4) $ 1/a_n = 2^{n-1} $ 發散，錯誤。
(5) $ \log a_n = (n-1)\log(1/2) = -(n-1)\log 2 $ 發散到 $-\infty$，錯誤。
答案為 (1)(2)(3)。報錯
 ChatGPT DeepSeek

加最愛

109指考數學乙(補考)試題-_C

某實驗室有輻射外洩，危害附近環境。根據調查：該輻射第一天汙染區域是一個以實驗室為中心，半徑2公里的圓形區域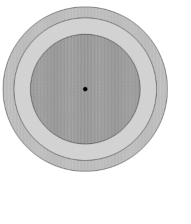，如圖中最內圓的圓內區域。第二天與第三天汙染區域逐漸擴大，都是以實驗室為中心，但汙染半徑越來越大的圓形區域，如圖中第二個與第三個同心圓的圓內區域。已知輻射每天汙染區域依照上述同心圓的模式向外擴大區域，而且新增汙染區域之面積都是前一天新增汙染區域面積的 $ \frac{5}{7} $ 倍，在汙染一直持續下去的條件下，全部汙染區域會趨近於半徑為 $ \sqrt{14 \times 13} $ 公里的圓形區域。

答案

第一天新增面積：$ \pi(2)^2=4\pi $
第二天新增面積：$ 4\pi\times\frac{5}{7} $
第三天新增面積：$ 4\pi\times(\frac{5}{7})^2 $
總面積 = $ 4\pi[1+\frac{5}{7}+(\frac{5}{7})^2+\cdots] = 4\pi\times\frac{1}{1-\frac{5}{7}} = 4\pi\times\frac{7}{2} = 14\pi $
設半徑為 $ R $，則 $ \pi R^2=14\pi $ ⇒ $ R=\sqrt{14} $
答案：$ \sqrt{14} $ 報錯
 ChatGPT DeepSeek

加最愛

114分科測驗數學甲試卷-05

有一實數數列 $\lt a_n\gt$，其中 $a_n=\cos(n\pi-\frac{\pi}{6})$，$n$ 為正整數。試選出正確的選項？
(1) $a_1=-\frac{1}{2}$
(2) $a_2=a_3$
(3) $a_4=a_{24}$
(4) $\lt a_n\gt $ 為收斂數列，且 $\lim\limits_{n \to \infty}a_n\lt1$
(5) $\sum\limits_{n=1}^{\infty}(a_n)^n=3-2\sqrt{3}$

答案

1. 化簡 $a_n=(-1)^n\cos\frac{\pi}{6}=(-1)^n\cdot\frac{\sqrt{3}}{2}$；
2. (1) $a_1=-\frac{\sqrt{3}}{2}\neq-\frac{1}{2}$，錯；
3. (2) $a_2=\frac{\sqrt{3}}{2}$，$a_3=-\frac{\sqrt{3}}{2}$，不相等，錯；
4. (3) $a_4=\frac{\sqrt{3}}{2}$，$a_{24}=\frac{\sqrt{3}}{2}$，相等，對；
5. (4) 數列交替取 $\pm\frac{\sqrt{3}}{2}$，不收斂，錯；
6. (5) 級數和 = $ \frac{-\sqrt{3}/2}{1 + \sqrt{3}/2} = 3 - 2\sqrt{3} $。答案：(3)(5) 報錯
 ChatGPT DeepSeek試題內容
 試題內容
 選擇(填)題答案
 非選擇題評分原則

加最愛

Saved articles