[題組:第3-4題]
假設棒球的旋轉與空氣阻力可被忽略,回答第3-4題有關棒球的問題。
某職棒投手先以固定力將靜止的棒球沿直線帶動約 1.5 m 的長度後,投出 144 km/h 的快速直球。已知棒球的質量約為 150 g,則該投手施於球的固定力量值約為何?
(A) 80 N
(B) 100 N
(C) 110 N
(D) 120 N
(E) 130 N。
牛頓第二定律
110指考物理分科考科_06
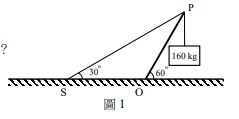
圖1為起重機示意圖,起重機臂 \( PO \) 和水平線的夾角為60°,且可繞O點自由轉動,其質量為200 kg且分布均勻,鋼索PS段和水平線的夾角為30°,\( PSO \) 位於垂直面。起重機臂右端懸掛一質量為160 kg的重物,若此時處於平衡狀態,且整條鋼索質量可忽略不計,則鋼索上的張力是多少N?(取重力加速度 \( g = 10 \text{m/s}^2 \))
(A)1600
(B)2600
(C)3200
(D)3600
(E)5200
略解:以 O 為支點,合力矩為零。
起重機臂重 \( Mg = 2000 \text{N} \),作用於中點。
重物重 \( mg = 1600 \text{N} \)。
設 OP 長 \( \ell \),張力 T 的力臂為 \( \ell \sin 30^\circ = \frac{\ell}{2} \)。
力矩平衡:\( T \cdot \frac{\ell}{2} = Mg \cdot \frac{\ell}{2} \cos 60^\circ + mg \cdot \ell \cos 60^\circ \)。
\( \frac{T}{2} = 2000 \times \frac{1}{4} + 1600 \times \frac{1}{2} = 500 + 800 = 1300 \Rightarrow T = 2600 \text{N} \)。
答案:B
110指考物理分科考科_15
[題組:第14-15題]
當地震表面波在稍後到達某地區時,假設固定於地面的物體僅作水平方向的簡譜運動,其振幅為 0.20 cm,週期為 0.40 s,最大加速度量值為 \( a \text{m/s}^2 \)。若固定於地面的水平書架上的書本不會因地震而滑動,則書本與書架板間的靜摩擦係數不能小於 \(\mu\)。以下各組 \((a, \mu)\) 數值,何者正確?(取重力加速度 g = 10 m/s^2)
(A) (0.25, 0.050) (B) (0.50, 0.050) (C) (0.50, 0.10) (D) (1.0, 0.10) (E) (1.5, 0.15)。
略解:簡諧運動最大加速度 \( a = \omega^2 A = \left( \frac{2\pi}{T} \right)^2 A = \left( \frac{2\pi}{0.4} \right)^2 \times 0.002 \approx (15.7)^2 \times 0.002 \approx 0.493 \text{m/s}^2 \approx 0.50 \text{m/s}^2 \)。
書本不滑動條件:\( ma \leq \mu mg \Rightarrow a \leq \mu g \Rightarrow \mu \geq \frac{a}{g} = \frac{0.50}{10} = 0.05 \)。
故 \( (a, \mu) = (0.50, 0.050) \)。
答案:B
110指考物理分科考科_22
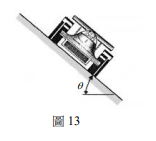
質量為 \( m \) 的汽車在與水平面夾角為 \( \theta \) 的斜面跑道作半徑為 \( R \) 的圓周運動,其面對車頭直視時的示意圖如圖 13 所示。設重力加速度的量值為 \( g \),下列敘述哪些正確?
(A)若夾角 \( \theta = 0 \),無摩擦力則無法作圓周運動
(B)需摩擦力克服沿斜面的下滑力 \( mg\sin\theta \) 才可作圓周運動
(C)無摩擦力也可作圓周運動,此時斜面跑道對車的正向力為 \( mg\cos\theta \)
(D)無摩擦力也可作圓周運動,此時速率 \( v = \sqrt{Rg \tan\theta} \)
(E)沿斜面向下的摩擦力可增加作圓周運動的向心力。
略解:(A)正確,\( \theta=0 \) 時,若無摩擦力,無水平力提供向心力。
(B)錯誤,鉛直方向力平衡,水平方向合力提供向心力,與下滑力無關。
(C)錯誤,無摩擦力時,鉛直方向 \( N\cos\theta = mg \Rightarrow N = \frac{mg}{\cos\theta} \)。
(D)正確,無摩擦力時,水平方向 \( N\sin\theta = m\frac{v^2}{R} \Rightarrow \frac{mg}{\cos\theta} \sin\theta = m\frac{v^2}{R} \Rightarrow v = \sqrt{Rg\tan\theta} \)。
(E)正確,摩擦力沿斜面向下時,其水平分量可增加向心力。
答案:A, D, E
110指考物理分科考科_26
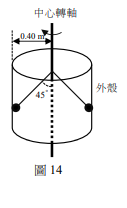
二、調速器可用來控制馬達的轉速,其結構如圖14所示,圓筒狀的外殼固定不動,中心轉軸隨馬達旋轉,軸上兩側各有一質量可忽略的短棒,其上端與中心轉軸連接,下端各有一個質量為1.0kg的擺錘,兩短棒與中心轉軸按在同一平面,且此平面隨中心轉軸旋轉時,短棒可以自由張開或合攏,當張角為45°時,擺錘恰可觸及外殼;當轉速夠大時擺錘會貼著外殼,對外殼施力,以傳達馬達轉速過大的訊息。已知外殼的內半徑為0.40m,重力加速度g=10m/s\(^2\)。
1. 當擺錘恰可觸及外殼而不對外殼施力時,計算此時中心轉軸的角速度。(4分)
2. 當中心轉軸以角速度6rad/s旋轉時,計算任一擺錘對外殼施加的正向力量值。(3分)
3. 若擺錘和外殼間的動摩擦係數μ=0.25,當中心轉軸的角速度維持6rad/s時,計算任一擺錘因摩擦而損耗的功率。(3分)
略解:1. 擺錘恰觸外殼不受力時,張角 \( \theta = 45^\circ \),半徑 \( r = 0.40 \text{m} \)。
受力分析:張力 \( T \),重力 \( mg \),向心力 \( m\omega^2 r \)。
\( T \cos\theta = mg \),\( T \sin\theta = m\omega^2 r \)。
兩式相除得 \( \tan\theta = \frac{\omega^2 r}{g} \Rightarrow \omega = \sqrt{\frac{g \tan\theta}{r}} = \sqrt{\frac{10 \times \tan 45^\circ}{0.40}} = \sqrt{25} = 5 \text{rad/s} \)。
2. 當 \( \omega = 6 \text{rad/s} \gt 5 \text{rad/s} \),擺錘貼外殼,設正向力 \( N \)。
水平:\( T\sin\theta + N = m\omega^2 r \)
鉛直:\( T\cos\theta = mg \)
由鉛直式 \( T = \frac{mg}{\cos\theta} \),代入水平式:
\( \frac{mg}{\cos\theta} \sin\theta + N = m\omega^2 r \Rightarrow mg\tan\theta + N = m\omega^2 r \)
\( N = m(\omega^2 r - g\tan\theta) = 1.0 \times (6^2 \times 0.40 - 10 \times 1) = 1.0 \times (14.4 - 10) = 4.4 \text{N} \)。
3. 動摩擦力 \( f_k = \mu N = 0.25 \times 4.4 = 1.1 \text{N} \)。
擺錘線速度 \( v = \omega r = 6 \times 0.40 = 2.4 \text{m/s} \)。
摩擦損耗功率 \( P = f_k v = 1.1 \times 2.4 = 2.64 \text{W} \)。
答案:1. \( 5 \text{rad/s} \) 2. \( 4.4 \text{N} \) 3. \( 2.64 \text{W} \)
111物理分科測驗–01
111物理分科測驗–12
在水平地面上,以不可伸長的細繩繞過定滑輪,將質量分別為 \( m_1 \)、\( m_2 \) 的上、下兩個均質箱子連接如圖4。已知重力加速度為 \( g \),細繩與滑輪之間無摩擦力,且其質量均可忽略,下箱之上、下表面的動摩擦係數皆為 \( \mu \),若下箱受到水平拉力 \( F \) 時,兩箱不轉動,均以等速度水平移動,則下列敘述哪些正確?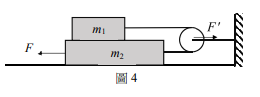
(A)地面施於下箱的正向力為 \( (m_1 + m_2)g \)
(B)施於下箱的水平拉力 \( F = \mu(3m_1 + m_2)g \)
(C)所有作用於上箱的水平力所產生的力矩為零
(D)所有作用於上箱的垂直力所產生的力矩為零
(E)右邊支架施予滑輪的水平力量值 \( F’ \),一定小於 \( F \)
(A)對:下箱鉛直力平衡,\( N_2 = (m_1 + m_2)g \)。(B)對:上箱水平力平衡 \( T = f_{k1} = \mu m_1 g \)。下箱水平力平衡 \( F = f_{k1} + T + f_{k2} = \mu m_1 g + \mu m_1 g + \mu (m_1 + m_2)g = \mu(3m_1 + m_2)g \)。(C)(D)錯:上箱合力矩為零,但水平力與垂直力各自產生的力矩不為零,但合力矩為零。(E)對:滑輪水平力 \( F' = 2T = 2\mu m_1 g < F \)。選(A)(B)(E)。
112物理分科測驗–14
某生練習紙牌魔術,將一疊紙牌水平整齊放置在桌面上,用右手食指以量值為N的正向力向下壓,然後向前水平推動,除了最上方數來第一張紙牌向前水平滑出之外,其他的紙牌皆不動。維持在原來的位置上。假設每一張紙牌的質量皆為$m$,紙牌與紙牌之間的靜摩擦係數與動摩擦係數分別為$μ_s$與$μ_k$,第一張紙牌與第二張紙牌之間作用力的水平分量量值為$F_{12}$,第二張紙牌與第三張紙牌之間作用力的水平分量量值為$F_{23}$,以此類推。令重力加速度為$g$,且只考慮摩擦力,重力與手指下壓的力,則下列關於第一張紙牌滑出之過程中的選項哪些正確?
(A) \( F_{12} = F_{23} \)
(B) \( F_{12} = \mu_k (N + 2mg) \)
(C) \( F_{23} = \mu_k (N + 2mg) \)
(D) \( F_{23} \leq \mu_k (N + 2mg) \)
(E) \( F_{12} = \mu_k (N + mg) \)
113物理分科測驗07
圖2為「電流天平」實驗裝置的示意圖,將U形電路PQRS放入螺線管內,其中長度為L的QR段約位於螺線管內的中央位置。螺線管所載電流為I_1,通過U形電路PQRS的電流為I_2,天平右臂受有磁力的作用,而左臂未端掛有小重物。下列有關此電流天平的敘述何者正確?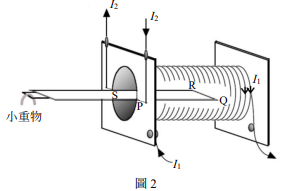
(A)U形電路所受的總磁力正比於I_1與I_2的乘積
(B)U形電路上所受的總磁力正比於U形電路於螺線管內的總長度
(C)螺線管電路必須與U形電路串聯,形成電流通路
(D)電流天平的兩臂達平衡時,若增加螺線管線圈匝數,不會改變其平衡狀態
(E)若小重物之重量不管如何調整,天平左臂一直下垂,則同時改變I_1和I_2的電流方向,可使天平趨於水平
113物理分科測驗08
以等長細繩懸掛半徑均為 \( r \)、質量均為 \( m \) 的兩相同金屬小球於固定點 \( O \),兩小球帶電量相同,因互斥分開,達到平衡後,球心相距 \( 2D (r \ll D) \),如圖3所示。若固定點到球心連線的垂直距離為 \( L \),庫侖常數為 \( k_e \),重力加速度為 \( g \),細繩質量可忽略,則每顆球上的電量約為下列何者?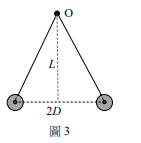
(A) \( 2\sqrt{\frac{mgD^3}{k_eL}} \)
(B) \( \sqrt{\frac{mgD^3}{k_eL}} \)
(C) \( \frac{1}{2}\sqrt{\frac{mgD^3}{k_eL}} \)
(D) \( 2\sqrt{\frac{k_eL}{mgD^3}} \)
(E) \( \sqrt{\frac{k_eL}{mgD^3}} \)