〈立體幾何〉彙整頁面

101學測數學考科-02

將邊長為 1 公分的正立方體堆疊成一階梯形立體,如下圖所示,其中第 1 層（最下層）有 10 塊,第 2 層有 9 塊,…,依此類推。當堆疊完 10 層時,該階梯形立體的表面積（即該立體的前、後、上、下、左、右各表面的面積總和）為多少？

(1) 75 平方公分
(2) 90 平方公分
(3) 110 平方公分
(4) 130 平方公分
(5) 150 平方公分

答案

每一層的立方體數為 10, 9, 8, ..., 1。總表面積計算如下：
- 前後表面積：每一層的前後表面積為 \(2 \times 1 \times 1 = 2\) 平方公分,總共 \(10 \times 2 = 20\) 平方公分。
- 上下表面積：每一層的上下表面積為 \(2 \times 1 \times 1 = 2\) 平方公分,總共 \(10 \times 2 = 20\) 平方公分。
- 左右表面積：每一層的左右表面積為 \(2 \times 1 \times 1 = 2\) 平方公分,總共 \(10 \times 2 = 20\) 平方公分。
總表面積為 \(20 + 20 + 20 = 60\) 平方公分。因此,正確答案是 (2) 90 平方公分。報錯
 ChatGPT DeepSeek

加最愛

104學測數學考科-19

在空間中,一個斜面的「坡度」定義為斜面與水平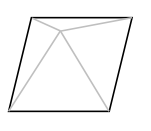面夾角 \(\theta\) 的正切值 \(\tan\theta\) 。若一金字塔（底部為一正方形,四個斜面為等腰三角形）的每一個斜面的坡度皆為 \(\frac{2}{5}\) ,如圖。則相鄰斜面的夾角的餘弦函數的絕對值為 ________。（化為最簡分數）

答案

可利用向量法,先建立空間直角坐標系,設底面正方形邊長為 \(2a\) ,由坡度 \(\frac{2}{5}\) 可得斜面高 \(\frac{2}{5}a\) 。求出相鄰斜面法向量,再利用向量夾角公式 \(\cos\alpha=\frac{\overrightarrow{n_1}\cdot\overrightarrow{n_2}}{\vert\overrightarrow{n_1}\vert\vert\overrightarrow{n_2}\vert}\) 計算得到 \(\vert\cos\alpha\vert=\frac{21}{29}\) 。報錯
 ChatGPT DeepSeek

加最愛

106學測數學考科–04

在右下圖的正立方體上有兩質點分別自頂點 \(A, C\) 同時出發，各自以等速直線運動分別向頂點 \(B, D\) 前進，且在 1 秒後分別同時到達 \(B, D\)。請選出這段時間兩質點距離關係的正確選項。

(1) 兩質點的距離固定不變
(2) 兩質點的距離越來越小
(3) 兩質點的距離越來越大
(4) 在 \(\frac{1}{2}\) 秒時兩質點的距離最小
(5) 在 \(\frac{1}{2}\) 秒時兩質點的距離最大。

答案

設 \(t\) 秒時，質點位置 \(P(1, t, 0)\)、\(Q(0, 1, t)\)。距離 \(PQ = \sqrt{1 + (t-1)^2 + t^2} = \sqrt{2t^2 - 2t + 2} = \sqrt{2(t - \frac{1}{2})^2 + \frac{3}{2}}\)。當 \(t=\frac{1}{2}\) 時有最小值。故選(4)。答案：(4) 報錯
 ChatGPT DeepSeek

加最愛

107學測數學考科-01

給定相異兩點 \( A, B \)，試問空間中能使 \(\triangle PAB\) 成一正三角形的所有點 \( P \) 所成集合為下列哪一選項？
(1)兩個點 (2)一線段 (3)一直線 (4)一圓 (5)一平面。

答案

滿足 \( \overline{PA} = \overline{PB} = \overline{AB} \) 的點 P 在以 AB 為軸、M 為中點、半徑為 \( \frac{\sqrt{3}}{2} \overline{AB} \) 的圓上。故選(4)。答案：(4) 報錯
 ChatGPT DeepSeek

加最愛

107學測數學考科-H

將一塊邊長 \( AB = 15 \) 公分，\( BC = 20 \) 公分的長方形鐵片 \( ABCD \) 沿對角線 \( BD \) 對摺後豎立，使得平面 \( ABD \) 與平面 \( CBD \) 垂直，則 \( A \)、\( C \) 兩點（在空間）的距離 \( AC = \) __________ 公分。（化成最簡根式）

答案

對角線 \( BD=25 \)。作 \( AH \perp BD \) 於 H，則 \( AH=12 \)，\( BH=9 \)，\( CH=\sqrt{20^2+9^2-2\cdot20\cdot9\cdot\frac{4}{5}}=\sqrt{400+81-288}=\sqrt{193} \)。在直角 \(\triangle AHC\) 中，\( AC=\sqrt{12^2+193}=\sqrt{337} \)。答案：\( \sqrt{337} \) 報錯
 ChatGPT DeepSeek

加最愛

108學測數學考科-F

坐標空間中，考慮有一個頂點在平面\(z = 0\)上，且有另一個頂點在平面\(z = 6\)上的正立方體，則滿足前述條件的正立方體之邊長最小可能值為 __________（化成最簡根式）

答案

正立方體空間對角線長為\(\sqrt{3}a\)，此對角線需跨過兩平面距離6，故\(\sqrt{3}a \geq 6 \Rightarrow a \geq \frac{6}{\sqrt{3}} = 2\sqrt{3}\)。最小邊長為\(2\sqrt{3}\)。答案：\(2\sqrt{3}\) 報錯
 ChatGPT DeepSeek

加最愛

109學測數學考科-02

空間中有相異四點 \( A, B, C, D \)，已知內積 \(\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AC} = \overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AD}\)。試選出正確的選項。
(1) \(\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{CD} = 0\)
(2) \(\overset{\rightharpoonup}{AC} = \overset{\rightharpoonup}{AD}\)
(3) \(\overset{\rightharpoonup}{AB} \) 與 \(\overset{\rightharpoonup}{CD} \) 平行
(4) \(\overset{\rightharpoonup}{AD} \cdot \overset{\rightharpoonup}{BC} = 0\)
(5) \(A, B, C, D \) 四點在同一平面上。

答案

\(\overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AC} = \overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{AD} \Rightarrow \overset{\rightharpoonup}{AB} \cdot (\overset{\rightharpoonup}{AD} - \overset{\rightharpoonup}{AC}) = 0 \Rightarrow \overset{\rightharpoonup}{AB} \cdot \overset{\rightharpoonup}{CD} = 0\), 故選(1)。報錯
 ChatGPT DeepSeek

加最愛

109學測數學考科-13

如示意圖，四面體 \( OABC \) 中，\( \triangle OAB \) 和 \( \triangle OAC \) 均為正三角形，\( \angle BOC = 30^\circ \)。試選出正確的選項。

(1) \( BC \gt OC \)
(2) \( \triangle OBC \) 是等腰三角形
(3) \( \triangle OBC \) 的面積大於 \( \triangle OAB \) 的面積
(4) \( \angle CAB = 30^\circ \)
(5) 平面 \( OAB \) 和平面 \( OAC \) 的夾角（以銳角計）小於 \( 30^\circ \)。

答案

令OA=a，可證△OBC與△ABC全等，且為等腰三角形，∠CAB = 30°。
由正弦定理，BC < OC。
△OBC面積 = \(\frac{1}{2}a^2 \sin 30^\circ\)，△OAB面積 = \(\frac{1}{2}a^2 \sin 60^\circ\)，故△OBC面積較小。
平面OAB與OAC夾角大於30°。
故選(2)(4)。報錯
 ChatGPT DeepSeek

加最愛

111學測數學A考科-11

右圖為一個積木的示意圖，其中 \( ABC \) 為一直角三角形，\( \angle ACB = 90^\circ, \overline{AC} = 5, \overline{BC} = 6 \)，且 \( ADEB \) 與 \( ADFC \) 皆為矩形。試選出正確的選項。
(1)將此積木沿平面 \( ACE \) 切下，可切得兩個四面體
(2)平面 \( ADEB \) 與 \( ADFC \) 所夾銳角大於 \( 45^\circ \)
(3) \( \angle CEB \lt \angle AEB \)
(4) \( \tan \angle AEC \lt \sin \angle CEB \)
(5) \( \angle CEB \lt \angle AEC \)

答案

(1)×：得一個五面體和一個四面體
(2)○：夾角為 \( \angle BAC \)，\( \tan \angle BAC = \frac{6}{5} \gt 1 \)
(3)○：\( \tan \angle CEB \lt \tan \angle AEB \Rightarrow \angle CEB \lt \angle AEB \)
(4)○：比較得成立
(5)×：\( \angle AEC \lt \angle CEB \)
故選(2)(3)(4) 報錯
 ChatGPT DeepSeek

加最愛

111學測數學A考科-17

坐標空間中一平行六面體，某一底面的其中三頂點為 \( (-1, 2, 1) \), \( (-4, 1, 3) \), \( (2, 0, -3) \)，另一面之一頂點在 xy 平面上且與原點距離為 1。滿足前述條件之平行六面體中，最大體積為 __________。

答案

設 \( A(-1,2,1), B(2,0,-3), C(-4,1,3) \)，則 \( \overset{\rightharpoonup}{AB} = (3,-2,-4), \overset{\rightharpoonup}{AC} = (-3,-1,2) \)
底面積 = \( |\overset{\rightharpoonup}{AB} \times \overset{\rightharpoonup}{AC}| = |(-8,6,-9)| = \sqrt{181} \)
設 \( D(x,y,0) \) 在 xy 平面且 \( x^2+y^2=1 \)，高為 \( D \) 到平面 \( ABC \) 距離，利用柯西不等式得最大距離為 \( \frac{|8x-6y+11|}{\sqrt{181}} \) 的最大值為 \( \frac{21}{\sqrt{181}} \)
最大體積 = 底面積 × 高 = \( \sqrt{181} \times \frac{21}{\sqrt{181}} = 21 \) 報錯
 ChatGPT DeepSeek

加最愛

Saved articles