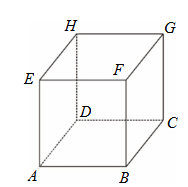
坐標空間中有一個正立方體ABCDEFGH ,試證明向量\(\overrightarrow{AG}\)與平面BDE垂直。(2分)
[非選擇題]立體幾何
107指考數學甲試題-4)
坐標空間中有一個正立方體ABCDEFGH ,承(3),試求出G點的坐標。(4分)
[非選擇題]由(2)知\(\overrightarrow{AG}\)與平面BDE垂直,所以\(\overrightarrow{AG}\)平行於平面BDE的法向量\(\overrightarrow{n}=(2,2,-1)\)(平面2x + 2y - z = -7的法向量)。
設G點坐標為\((x,y,z)\),則\(\overrightarrow{AG}=(x - 2,y - 2,z - 6)\)。
因為\(\overrightarrow{AG}\)與\(\overrightarrow{n}=(2,2,-1)\)平行,所以\(\frac{x - 2}{2}=\frac{y - 2}{2}=\frac{z - 6}{-1}=k\)(k為常數),即\(x = 2k + 2\),\(y = 2k + 2\),\(z = -k + 6\)。
又由(3)知A點到平面BDE的距離是3,且G點到平面BDE的距離與A點到平面BDE的距離相等(正立方體性質)。
將G點坐標\((2k + 2,2k + 2,-k + 6)\)代入點到平面的距離公式\(d=\frac{\vert2(2k + 2)+2(2k + 2)-(-k + 6)+7\vert}{\sqrt{2^{2}+2^{2}+(-1)^{2}}}=3\)。
\(\frac{\vert4k + 4 + 4k + 4 + k - 6 + 7\vert}{3}=3\),\(\vert9k + 9\vert = 9\),即\(9k + 9 = 9\)或\(9k + 9 = -9\)。
解得\(k = 0\)或\(k = -2\),\(k = 0\)時不滿足G與A不重合,所以\(k = -2\)。
則\(x = 2\times(-2)+2=-2\),\(y = 2\times(-2)+2=-2\),\(z = -(-2)+6 = 8\)。
所以G點坐標為(-2,-2,8)。 報錯
ChatGPT DeepSeek
107指考數學甲試題-1)
坐標空間中有一個正立方體ABCDEFGH ,試證明A點到平面BDE的距離是對角線AG長度的三分之一。(4分)
[非選擇題]設正立方體的稜長為a。
以A為原點,分別以AB、AD、AE所在直線為x、y、z軸建立空間直角坐標系。
則A(0,0,0),B(a,0,0),D(0,a,0),E(0,0,a),G(a,a,a)。
可求得平面BDE的法向量\(\overrightarrow{n}\):
\(\overrightarrow{BD}=(-a,a,0)\),\(\overrightarrow{BE}=(-a,0,a)\)。
設\(\overrightarrow{n}=(x,y,z)\),由\(\overrightarrow{n}\cdot\overrightarrow{BD}=0\)且\(\overrightarrow{n}\cdot\overrightarrow{BE}=0\),可得\(\begin{cases}-ax + ay = 0\\-ax + az = 0\end{cases}\),令x = 1,解得y = 1,z = 1,所以\(\overrightarrow{n}=(1,1,1)\)。
\(\overrightarrow{AG}=(a,a,a)\),\(\vert\overrightarrow{AG}\vert=\sqrt{a^{2}+a^{2}+a^{2}}=\sqrt{3}a\)。
A點到平面BDE的距離\(d=\frac{\vert\overrightarrow{AB}\cdot\overrightarrow{n}\vert}{\vert\overrightarrow{n}\vert}\),\(\overrightarrow{AB}=(a,0,0)\),則\(d=\frac{\vert a\times1 + 0\times1 + 0\times1\vert}{\sqrt{1^{2}+1^{2}+1^{2}}}=\frac{a}{\sqrt{3}}\)。
所以A點到平面BDE的距離\(d=\frac{1}{3}\vert\overrightarrow{AG}\vert\),即A點到平面BDE的距離是對角線AG長度的三分之一。 報錯
ChatGPT DeepSeek
107指考數學甲試題-2)
坐標空間中有一個正立方體ABCDEFGH ,試證明向量\(\overrightarrow{AG}\)與平面BDE垂直。(2分)
[非選擇題]107指考數學甲試題-4)
坐標空間中有一個正立方體ABCDEFGH ,承(3),試求出G點的坐標。(4分)
[非選擇題]由(2)知\(\overrightarrow{AG}\)與平面BDE垂直,所以\(\overrightarrow{AG}\)平行於平面BDE的法向量\(\overrightarrow{n}=(2,2,-1)\)(平面2x + 2y - z = -7的法向量)。
設G點坐標為\((x,y,z)\),則\(\overrightarrow{AG}=(x - 2,y - 2,z - 6)\)。
因為\(\overrightarrow{AG}\)與\(\overrightarrow{n}=(2,2,-1)\)平行,所以\(\frac{x - 2}{2}=\frac{y - 2}{2}=\frac{z - 6}{-1}=k\)(k為常數),即\(x = 2k + 2\),\(y = 2k + 2\),\(z = -k + 6\)。
又由(3)知A點到平面BDE的距離是3,且G點到平面BDE的距離與A點到平面BDE的距離相等(正立方體性質)。
將G點坐標\((2k + 2,2k + 2,-k + 6)\)代入點到平面的距離公式\(d=\frac{\vert2(2k + 2)+2(2k + 2)-(-k + 6)+7\vert}{\sqrt{2^{2}+2^{2}+(-1)^{2}}}=3\)。
\(\frac{\vert4k + 4 + 4k + 4 + k - 6 + 7\vert}{3}=3\),\(\vert9k + 9\vert = 9\),即\(9k + 9 = 9\)或\(9k + 9 = -9\)。
解得\(k = 0\)或\(k = -2\),\(k = 0\)時不滿足G與A不重合,所以\(k = -2\)。
則\(x = 2\times(-2)+2=-2\),\(y = 2\times(-2)+2=-2\),\(z = -(-2)+6 = 8\)。
所以G點坐標為(-2,-2,8)。 報錯
ChatGPT DeepSeek
109指考數學甲(補考)試題-3)
“設\(f(x)=x^{3}+bx^{2}+cx + d\)為三次實係數多項式函數。已知\(f'(x)\)是\(f(x)\)的因式,若知\(f(-1)=0\),試
[非選擇題]已知\(B(1,1,0)\),\(\overline{BQ}=t\),且\(F(1,1,1)\),則\(Q\)點坐標為\((1,1,t)\)。
又\(A(1,0,0)\),\(P(0,1,\frac{1}{2})\),因為\(A\)、\(Q\)、\(P\)、\(R\)為平行四邊形的四個頂點,所以\(\overrightarrow{AQ}=\overrightarrow{PR}\)。
\(\overrightarrow{AQ}=(1,1,t)-(1,0,0)=(0,1,t)\)。
設\(R(x,y,z)\),\(\overrightarrow{PR}=(x,y,z)-(0,1,\frac{1}{2})=(x,y - 1,z-\frac{1}{2})\)。
由\(\overrightarrow{AQ}=\overrightarrow{PR}\)可得\(\begin{cases}x = 0\\y - 1 = 1\\z-\frac{1}{2}=t\end{cases}\),解得\(\begin{cases}x = 0\\y = 2\\z=t + \frac{1}{2}\end{cases}\),即\(R(0,2,t+\frac{1}{2})\)。
所以\(\overrightarrow{AR}=(0,2,t+\frac{1}{2})-(1,0,0)=(-1,2,t+\frac{1}{2})\)。 報錯
ChatGPT DeepSeek
109指考數學甲試題-1)
一個邊長為1的正立方體\(ABCD – EFGH\),點\(P\)為稜邊\(\overline{CG}\)的中點,點\(Q\)、\(R\)分別在稜邊\(\overline{BF}\)、\(\overline{DH}\)上,且\(A\)、\(Q\)、\(P\)、\(R\)為一平行四邊形的四個頂點。今設定坐標系,使得\(D\)、\(A\)、\(C\)、\(H\)的坐標分別為\((0,0,0)\)、\((1,0,0)\)、\((0,1,0)\)、\((0,0,1)\),且\(\overline{BQ}=t\),試求點\(P\)的坐標。(2分)
[非選擇題]109指考數學甲試題-2)
一個邊長為1的正立方體\(ABCD – EFGH\),點\(P\)為稜邊\(\overline{CG}\)的中點,點\(Q\)、\(R\)分別在稜邊\(\overline{BF}\)、\(\overline{DH}\)上,且\(A\)、\(Q\)、\(P\)、\(R\)為一平行四邊形的四個頂點。今設定坐標系,使得\(D\)、\(A\)、\(C\)、\(H\)的坐標分別為\((0,0,0)\)、\((1,0,0)\)、\((0,1,0)\)、\((0,0,1)\),且\(\overline{BQ}=t\),試求向量\(\overrightarrow{AR}\)(以\(t\)的式子來表示)。(2分)
[非選擇題]