甲、乙兩計時器原來置於地球表面計時，甲計時器以在鉛垂面作小角度左右擺動的單擺週期，作為計時基準；乙計時器利用彈簧讓重物在光滑水平面上振動，以其週期作為計時基準。現將兩計時器移至另一星球表面，該星球表面的重力加速度量值為地球表面的4倍，則下列有關甲計時器擺動週期 \( T_{\text{甲}} \) 和乙計時器振動週期 \( T_{\text{乙}} \) 的敘述何者正確？（忽略空氣阻力）
(A) \( T_{\text{甲}} \cdot T_{\text{乙}} \) 均變為原來的4倍
(B) \( T_{\text{甲}} \cdot T_{\text{乙}} \) 均變為原來的1/2
(C) \( T_{\text{甲}} \) 變為原來的2倍，\( T_{\text{乙}} \) 不變
(D) \( T_{\text{甲}} \) 變為原來的1/2，\( T_{\text{乙}} \) 不變
(E) \( T_{\text{甲}} \cdot T_{\text{乙}} \) 均不變。
[題組:第14-15題]
當地震表面波在稍後到達某地區時，假設固定於地面的物體僅作水平方向的簡譜運動，其振幅為 0.20 cm，週期為 0.40 s，最大加速度量值為 \( a \text{m/s}^2 \)。若固定於地面的水平書架上的書本不會因地震而滑動，則書本與書架板間的靜摩擦係數不能小於 \(\mu\)。以下各組 \((a, \mu)\) 數值，何者正確？（取重力加速度 g = 10 m/s^2）
(A) (0.25, 0.050) (B) (0.50, 0.050) (C) (0.50, 0.10) (D) (1.0, 0.10) (E) (1.5, 0.15)。
略解：簡諧運動最大加速度 \( a = \omega^2 A = \left( \frac{2\pi}{T} \right)^2 A = \left( \frac{2\pi}{0.4} \right)^2 \times 0.002 \approx (15.7)^2 \times 0.002 \approx 0.493 \text{m/s}^2 \approx 0.50 \text{m/s}^2 \)。
書本不滑動條件：\( ma \leq \mu mg \Rightarrow a \leq \mu g \Rightarrow \mu \geq \frac{a}{g} = \frac{0.50}{10} = 0.05 \)。
故 \( (a, \mu) = (0.50, 0.050) \)。
答案：B 報錯
ChatGPT DeepSeek
某生設計了一個不需使用計時器而可量測重力加速度的實驗。他選用了一個彈力常數為 \(k\)，自然長度為 \(l\)，繁有質量為 \(m\) 之質點的彈簧，使其作水平面之簡諧運動。再以一個擺長為 \(L\)，擺鐘不計體積，質量為 \(M\) 的單擺，調整其擺長 \(L\)，使兩個系統之簡諧運動的週期相同，則其所測得的重力加速度量值為何？
(A) \(\frac{lM}{k}\)
(B) \(\frac{Lm}{k}\)
(C) \(\frac{LM}{k}\)
(D) \(\frac{lk}{M}\)
(E) \(\frac{Lk}{m}\)
2024年4月3日花蓮發生規模7.2的地震，台北101大樓僅有輕微晃動，這是由於92樓到87樓間設有以多條鋼鐵懸掛重量660公噸的球形質量塊，並以阻尼器與機板連接所構成的減振系統。原理為：可將前述減振系統視為有效擺長約為12.1m的單擺式減振系統（示意圖如圖4），並設計其振動頻率為接近大樓主結構的基頻。當風力或地震使大樓以主結構的基頻振動時，振動能量便能有效地轉移到朝相反方向移動的球形質量塊，使得阻尼器伸縮以吸收大樓的振動能量，如圖5所示。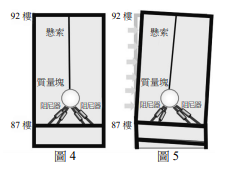
估算101大樓主結構以基頻振動的週期約為下列何者？（可將減振系統視為理想單擺，且取重力加速度 \( g = 10 \text{m/s}^2 \) 來估算）
(A) 1.1s
(B) 5.6s
(C) 6.9s
(D) 9.8s
(E) 14.0s
小角度的單擺擺動可視為簡諧運動。一個擺長0.20m的單擺作小角度的左右來回擺動，當擺鐘由左向右經過平衡位置時開始計時，經過1.5s後，下列關於單擺運動狀況的敘述何者正確？（取重力加速度為9.8m/s²）
(A)擺鐘向左運動且速率增加 (B)擺鐘向左運動且速率減少
(C)擺鐘向右運動且速率減少 (D)擺鐘向右運動且速率增加
(E)擺鐘向左作等速運動
