角速度

[題組:第19題到第21題] ◎2021年12月發射的James Webb太空望遠鏡（JWST）主要用於紅外線天文學的研究，是目前太空中最強大的望遠鏡，它的溫度必須保持低於50K，才可在不受其他熱輻射源的干擾下觀察微弱的紅外線信號。JWST的位置靠近日一地系統的拉格朗日點\(L_2\)，此為日一地連心線上的定點，位於地球公轉軌道外側，如圖10所示，其中實線的圓弧與圓分別代表地球與月球的公轉軌道。已知在\(L_2\)點的小物體，受到日一地系統的重力，可與地球同步繞日一地系統的質心公轉。假設只考慮來自日、地的重力，日一地的距離近似為定值\(R\)，日、地的質量分別為\(M \cdot m\)，地心到\(L_2\)的距離為\(r\)，重力常數為\(G\)，日一地系統繞其質心\(C\)轉動的角速度為\(\omega\)。注意：只有日一地系統的質心\(C\)可視為靜止，日、地與\(L_2\)處的小物體均繞\(C\)以角速度\(\omega\)做圓周運動。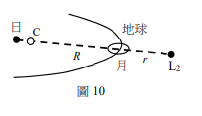
已知地心到\(C\)的距離為\(\frac{MR}{(M+m)}\)，則角速度率的平方\(\omega^2\)為下列何者？（單選）
(A) \(\omega^2 = G\frac{M+m}{r^3}\)
(B) \(\omega^2 = G\frac{M+m}{R^3}\)
(C) \(\omega^2 = G\frac{m}{r^3}\)
(D) \(\omega^2 = G\frac{m}{R^3}\)
(E) \(\omega^2 = G\frac{M}{r^3}\)

[題組:24-26題]
◎一台具有三段變速系統的腳踏車（如圖10），其前齒盤的齒數為38齒，後齒盤組有相同轉軸但齒數分別為14、19與26齒的3個齒盤。鍵條套在前齒盤和後齒盤上，當前齒盤轉動1齒，後齒輪盤也跟著轉動1齒；且齒盤齒數與齒盤半徑成正比。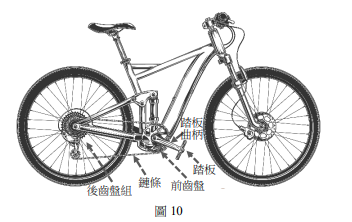
24 齒數為n的齒盤邊緣的切線速度定為\(v_n\)，角速度定為\(\omega_n\)，法線加速度（向心加速度）定為\(a_{Nu}\)。若變速系統將鍵條套在前齒盤與齒數19齒的後齒盤上，當前、後齒盤轉動時，下列敘述哪些正確？（多選）（5分）
(A)後齒盤：\(v_{26}/v_{14}=13/7\)
(B)後齒盤：\(\omega_{26}/\omega_{14}=7/13\)
(C)後齒盤：\(a_{N26}/a_{N14}=1\)
(D)前齒盤與後齒盤：\(\omega_{38}/\omega_{19}=1/2\)
(E)前齒盤與後齒盤：\(v_{38}/v_{19}=2\)

[55-57為題組]自古流傳：「種田無定例，全要靠節氣。」24節氣於2016年已正式列入聯合國教科文組織人類非物質文化遺產名錄，它的訂定是以24個節氣為分段點，將地球繞太陽公轉的軌道劃分為24段，相鄰兩節氣所對應之地球到太陽的連線，其夾角均為15°。北半球某年春夏秋冬四季中等角度間隔之相鄰兩節氣如圖10所示（僅為示意圖，未完全符合實際情況）。表4列出了各季節兩節氣之間的時距。假設表中相鄰兩節氣之間，地球與太陽連線平均每秒鐘掃過的角度分別為 \( \omega_{\text{春}} \)、\( \omega_{\text{夏}} \)、\( \omega_{\text{秋}} \)、\( \omega_{\text{冬}} \)，而平均每秒鐘掃過的面積分別為 \( \lambda_{\text{春}} \)、\( \lambda_{\text{夏}} \)、\( \lambda_{\text{秋}} \)、\( \lambda_{\text{冬}} \)。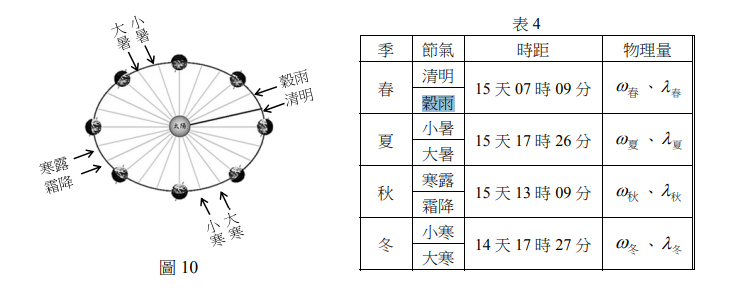
圖10
依據以上資料及克卜勒等面積定律，回答55-57題。
關於相鄰兩節氣之間地球與太陽連線平均每秒掃過的角度，下列敘述何者正確？
(A) \( \omega_{\text{春}} \) 最大
(B) \( \omega_{\text{夏}} \) 最大
(C) \( \omega_{\text{秋}} \) 最大
(D) \( \omega_{\text{冬}} \) 最大
(E) \( \omega_{\text{春}} \)、\( \omega_{\text{夏}} \)、\( \omega_{\text{秋}} \)、\( \omega_{\text{冬}} \) 都相等