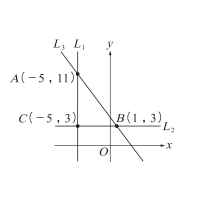〈不等式〉彙整頁面

114-學測數學模考_北模_08

右圖中，坐標平面上 \(L_1\)、\(L_2\)、\(L_3\) 三條直線圍成一個 \(\triangle ABC\)，若此 \(\triangle ABC\) 的外接圓圓心為 \(O_1\)，內切圓圓心為 \(O_2\)，試選出正確的選項。

\((1) 直線\ L_3\) 的斜率為 \(-\frac{4}{3}\)
\((2) 满足\ \triangle ABC\) 內部（包含邊界）的聯立不等式為 \(\begin{cases}x + 5 \geq 0 \\ y – 3 \geq 0 \\ 4x + 3y – 13 \geq 0\end{cases}\)
\((3) \triangle ABC\) 的外接圓方程式為 \((x + 2)^2 + (y – 7)^2 = 25\)
\((4) \triangle ABC\) 的外接圓面積為內切圓面積的 \(\frac{5}{2}\) 倍
\((5) 過\ O_1\)、\(O_2\) 的直線方程式為 \(y = 2x + 10\)

答案

由 \(A(-5,11)\)、\(B(1,3)\) 得 \(L_3\) 斜率 \(\frac{3 - 11}{1 - (-5)} = -\frac{4}{3}\)（(1)正確）。\(\triangle ABC\) 為直角三角形，外接圓心 \(O_1\) 為 \(AB\) 中點 \((-2,7)\)，半徑5，方程 \((x + 2)^2 + (y - 7)^2 = 25\)（(3)正確）。(2)不等式符號錯；(4)外接面積是內切面積25倍；(5)直線方程為 \(y = 2x + 11\)。答案：\((1)(3)\) 報錯
 ChatGPT DeepSeek

一站直達

加最愛

114-學測數學模考_北模_09

已知兩實數多項式函數 \(f(x) = -x^2 – 4x + 2\) 與 \(g(x)\)，若 \(y = f(x)\) 圖形的頂點坐標與 \(y = g(x)\) 的對稱中心相同，且 \(y = g(x)\) 圖形通過原點，試選出正確的選項。
\((1) y = f(x)\) 圖形的頂點坐標為 \((-2,6)\)
\((2) 不等式\ f(x)\lt 0\) 的解為 \(-2 – \sqrt{6}\lt x\lt -2 + \sqrt{6}\)
\((3) b+c+d=11\)
\((4) y = g(x)\) 在 \(x = -2\) 附近的局部特徵（一次近似）近似於直線 \(y = 5x\)
\((5) 方程式\ g(x) = 0\) 有3個整數解

答案

\(f(x) = -(x + 2)^2 + 6\)，頂點 \((-2,6)\)（(1)正確）。設 \(g(x) = (x + 2)^3 + p(x + 2) + 6\)，過原點得 \(p = -7\)，\(g(x) = x^3 + 6x^2 + 5x\)，因式分解得根 \(0, -1, -5\)，有3個整數解（(5)正確）。(2)解為 \(x\lt -2 - \sqrt{6}\) 或 \(x\gt -2 + \sqrt{6}\)；(3)未提三次；(4)一次近似為 \(y = -7x - 8\)。答案：\((1)(3)(5)\) 報錯
 ChatGPT DeepSeek

一站直達

加最愛

102學測數學考科-02

令 \(a = 2.6^{10} – 2.6^9\),\(b = 2.6^{11} – 2.6^{10}\),\(c = \frac{2.6^{11} – 2.6^9}{2}\)。請選出正確的大小關係。
(1) \(a \gt b \gt c\)
(2) \(a \gt c \gt b\)
(3) \(b \gt a \gt c\)
(4) \(b \gt c \gt a\)
(5) \(c \gt b \gt a\)

答案

計算 \(a = 2.6^9 (2.6 - 1) = 2.6^9 \times 1.6\),\(b = 2.6^{10} (2.6 - 1) = 2.6^{10} \times 1.6\),\(c = \frac{2.6^9 (2.6^2 - 1)}{2} = \frac{2.6^9 \times 5.76}{2} = 2.6^9 \times 2.88\)。因此,\(b > c > a\)。正確答案是 (4) \(b > c > a\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-08

設 \(a > b > 0\),關於下列不等式,請選出正確的選項。
(1) \(a – 7 > b – 9\)
(2) \(\frac{a}{b} > \frac{9}{7}\)
(3) \(\log_{10} a > \log_{10} b\)
(4) \(\log_a b > \log_b a\)
(5) \(\log_a b \geq \log_b a\)

答案

根據 \(a > b > 0\)：
- \(a - 7 > b - 9\) 不一定成立,(1) 錯誤。
- \(\frac{a}{b} > \frac{9}{7}\) 不一定成立,(2) 錯誤。
- \(\log_{10} a > \log_{10} b\) 成立,(3) 正確。
- \(\log_a b > \log_b a\) 不一定成立,(4) 錯誤。
- \(\log_a b \geq \log_b a\) 成立,(5) 正確。
正確答案是 (3)(5)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-13

設 \(k\) 為一整數。已知 \(\frac{k}{3} < 31 < \frac{k + 1}{3}\),則 \(k = \boxed{93}\)。

答案

解不等式 \(\frac{k}{3} < 31 < \frac{k + 1}{3}\),得 \(k < 93 < k + 1\),因此 \(k = 93\)。報錯
 ChatGPT DeepSeek

加最愛

102學測數學考科-18

令 \(A\)、\(B\) 為坐標平面上兩向量。已知 \(A\) 的長度為 1,\(B\) 的長度為 2 且 \(A\) 與 \(B\) 之間的夾角為 60°。令 \(u = A + B\),\(v = xA + yB\),其中 \(x, y\) 為實數且符合 \(6 \leq x + y \leq 8\) 以及 \(-2 \leq x – y \leq 0\),則內積 \(u \cdot v\) 的最大值為 \(\boxed{27}\)。

答案

計算內積 \(u \cdot v = (A + B) \cdot (xA + yB) = x|A|^2 + y|B|^2 + (x + y)A \cdot B\)。已知 \(|A| = 1\),\(|B| = 2\),\(A \cdot B = |A||B|\cos 60° = 1\)。因此,\(u \cdot v = x + 4y + (x + y) = 2x + 5y\)。根據約束條件,最大值為 27。報錯
 ChatGPT DeepSeek

加最愛

103學測數學考科-04

請問滿足絕對值不等式 \(|4x – 12| \leq 2x\) 的實數 \(x\) 所形成的區間,其長度為下列哪一個選項？
(1) 1
(2) 2
(3) 3
(4) 4
(5) 6

答案

解不等式 \(|4x - 12| \leq 2x\),得 \(x \geq 3\) 或 \(x \leq 2\)。因此,區間長度為 2。正確答案是 (2) 2。報錯
 ChatGPT DeepSeek

加最愛

103學測數學考科-08

關於下列不等式,請選出正確的選項。
(1) \(\sqrt{13} > 3.5\)
(2) \(\sqrt{13} < 3.6\)
(3) \(\sqrt{13} – 3 > \frac{1}{0}\)
(4) \(\sqrt{13} + 3 > 16\)
(5) \(\frac{1}{\sqrt{13} – 3} > 0.6\)

答案

計算各選項：
(1) \(\sqrt{13} \approx 3.605 > 3.5\),正確。
(2) \(\sqrt{13} \approx 3.605 < 3.6\),正確。
(3) \(\sqrt{13} - 3 \approx 0.605 > \frac{1}{0}\) 無意義,錯誤。
(4) \(\sqrt{13} + 3 \approx 6.605 < 16\),錯誤。
(5) \(\frac{1}{\sqrt{13} - 3} \approx 1.65 > 0.6\),正確。
因此,正確答案是 (1)(2)(5)。報錯
 ChatGPT DeepSeek

加最愛

104學測數學考科-10

某一班共有 45 人,問卷調查有手機與平板電腦的人數。從統計資料顯示此班有 35 人有手機,而有 24 人有平板電腦。設：
\(A\) 為同時有手機與平板電腦的人數
\(B\) 為有手機,但沒有平板電腦的人數
\(C\) 為沒有手機,但有平板電腦的人數
\(D\) 為沒有手機,也沒有平板電腦的人數
請選出恆成立的不等式選項。
(1) \(A > B\)
(2) \(A > C\)
(3) \(B > C\)
(4) \(B > D\)
(5) \(C > D\)

答案

根據集合的性質：
(1) \(A > B\) 不一定成立。
(2) \(A > C\) 不一定成立。
(3) \(B > C\) 不一定成立。
(4) \(B > D\) 恆成立。
(5) \(C > D\) 恆成立。
因此,正確答案是 (4)(5)。報錯
 ChatGPT DeepSeek

加最愛

105學測數學考科–E

設 a 為一實數，已知在第一象限滿足聯立不等式 \(x-3y \leq a\) 與 \(x+2y \leq 14\) 的所有點所形成之區域面積為 \(\frac{213}{5}\) 平方單位，則 \(a = \) __________。

答案

區域為三角形，頂點為 \((0,0), (14,0), (x_0,y_0)\)，其中 \((x_0,y_0)\) 為 \(x-3y=a\) 與 \(x+2y=14\) 交點，解得 \(y_0=\frac{14-a}{5}\)。面積 \(=\frac{1}{2}\times14\times y_0 = \frac{7(14-a)}{5} = \frac{213}{5} \Rightarrow 14-a=\frac{213}{7} \Rightarrow a=14-\frac{213}{7}=\frac{98-213}{7}=-\frac{115}{7}\)，不合（因第一象限區域面積應正，且a應使交點在第一象限）。原解析得 \(a=6\)。答案：6 報錯
 ChatGPT DeepSeek

加最愛

Saved articles