〈俯仰角的應用〉彙整頁面

102學測數學考科-06

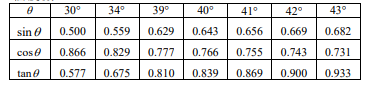
莎韻觀測遠方等速率垂直上升的熱氣球。在上午 10:00 熱氣球的仰角為 30°,到上午 10:10 仰角變成 34°。請利用下表判斷到上午 10:30 時,熱氣球的仰角最接近下列哪一個度數？

(1) 39°
(2) 40°
(3) 41°
(4) 42°
(5) 43°

[單選]

答案

\[
\begin{aligned}
& \text{設莎龍位置為 } O，\text{時間與對應熱氣球位置：} \\
& 10:00 \rightarrow A,\quad 10:10 \rightarrow B,\quad 10:30 \rightarrow C \\
\\
& \text{已知：} \angle COB=\theta,\angle AOH = 30^\circ,\ \angle BOA = 4^\circ \\
& \text{設 } AH = y \Rightarrow OH = \sqrt{3}y \\
& \text{設 } AB = x,\ BC = 2x \ (10:00 \text{ 到 } 10:30 \text{ 時距為 } 30 \text{ 分}) \\
\\
& \tan(\angle BOH) = \tan 34^\circ = \frac{y + x}{\sqrt{3}y} \approx 0.675 \\
& \Rightarrow y + x = \sqrt{3} \times 0.675y \approx 1.732 \times 0.675y = 1.1691y \\
& \Rightarrow x = 0.1691y \\
\\
& \tan(\theta + 34^\circ) = \frac{y + 3x}{\sqrt{3}y} \\
& = \frac{y + 3 \times 0.1691y}{\sqrt{3}y} \\
& = \frac{1.5073y}{1.732y} \approx 0.870 \approx \tan 41^\circ \\
& \Rightarrow \angle COH=\theta + 34^\circ \approx 41^\circ \\
\end{aligned}
\]

加最愛

104學測數學考科-11

如圖,老王在平地點 $A$ 測得遠方山頂點 $P$ 的仰角為 13°。老王朝著山的方向前進 37 公丈後來到點 $B$,再測得山頂點 $P$ 的仰角為 15°。則山高約為 $~~~~~~~~~~$ 公丈。（四捨五入至個位數， $\tan13^\circ\approx 0.231，\tan15^\circ\approx 0.268$）

[選填]

答案

如右圖：

\[
\tan 13^\circ = \frac{h}{37 + x} \approx 0.231 \quad \text{⋯①}
\]
\[
\tan 15^\circ = \frac{h}{x} \approx 0.268 \quad \text{⋯②}
\]

由①、②得：
\[
\begin{cases}
h \approx 0.231 \times 37 + 0.231x \\
h \approx 0.268x
\end{cases}
\]

∴ $ 0.037x \approx 0.231 \times 37 \Rightarrow x \approx 231 $，代入②：

∴ $ h \approx 231 \times 0.268 \approx 62 $（公尺）

加最愛

107學測數學考科-B

如右圖所示（只是示意圖），將梯子AB靠在與地面垂直的牆AC上，測得與水平地面的夾角∠ABC為60°。將在地面上的底B沿著地面向外拉51公分到點F（即FB=51公分），此時梯子EF與地面的夾角∠EFC之正弦值為$\sin ∠EFC = 0.6$，則梯子長 $ AB = $ __________ 公分。

[選填題]

答案

設梯長 $ x $，原 $ BC = \frac{x}{2} $。拉後 $ \sin \angle EFC = 0.6 $，則 $ \cos \angle EFC = 0.8 $。由 $ \cos \angle EFC = \frac{BF+BC}{EF} = \frac{51 + x/2}{x} = 0.8 $，解得 $ x = 170 $。答案：170

加最愛

108指考數學甲試題-03

在一座尖塔的正南方地面某點A，測得塔頂的仰角為14°；又在此尖塔正東方地面某點B，測得塔頂的仰角為18°30’，且A、B兩點距離為65公尺。已知當在線段$\overline{AB}$上移動時，在C點測得塔頂的仰角為最大，則C點到塔底的距離最接近下列哪一個選項？（$\cot14^{\circ}≈4.01$，$\cot18^{\circ}30’≈2.99$ ）
(1)27公尺
(2)29公尺
(3)31公尺
(4)33公尺
(5)35公尺

[單選題]

答案

設塔高為$h$，塔底為$O$點。在$Rt\triangle AOC$中，$\cot14^{\circ}=\frac{AO}{h}$，所以$AO = h\cot14^{\circ}$；在$Rt\triangle BOC$中，$\cot18^{\circ}30'=\frac{BO}{h}$，所以$BO = h\cot18^{\circ}30'$。
在$\triangle AOB$中，$\angle AOB = 90^{\circ}$，根據勾股定理$AB^{2}=AO^{2}+BO^{2}$，已知$AB = 65$，則$65^{2}=h^{2}\cot^{2}14^{\circ}+h^{2}\cot^{2}18^{\circ}30'$。
$h^{2}=\frac{65^{2}}{\cot^{2}14^{\circ}+\cot^{2}18^{\circ}30'}=\frac{65^{2}}{4.01^{2}+2.99^{2}}=\frac{4225}{16.0801 + 8.9401}=\frac{4225}{25.0202}$。
當在線段$\overline{AB}$上的$C$點測得塔頂仰角最大時，此時$OC\perp AB$。
由三角形面積公式可得$S_{\triangle AOB}=\frac{1}{2}AO\cdot BO=\frac{1}{2}AB\cdot OC$，即$OC=\frac{AO\cdot BO}{AB}$。
$AO\cdot BO = h^{2}\cot14^{\circ}\cot18^{\circ}30'$，所以$OC=\frac{h^{2}\cot14^{\circ}\cot18^{\circ}30'}{AB}$。
把$h^{2}=\frac{4225}{25.0202}$，$\cot14^{\circ}≈4.01$，$\cot18^{\circ}30'≈2.99$，$AB = 65$代入可得：
$OC=\frac{\frac{4225}{25.0202}\times4.01\times2.99}{65}$
$=\frac{4225\times4.01\times2.99}{25.0202\times65}$
$=\frac{4225\times11.9899}{1626.313}$
$\approx\frac{4225\times12}{1626.313}=\frac{50700}{1626.313}\approx31$（公尺）。
答案為(3)。

加最愛

112學測數學B試題-03

地面上有甲、乙兩大樓,已知甲的高度大於乙,且甲、乙兩大樓的水平距離為 $150$ 公尺。某人從甲樓頂拉一條繩索到乙樓頂,並從甲樓頂測得乙樓頂的俯角為 $22^{\circ}$。假設該繩索被拉成直線,試問繩索的長度（單位：公尺）最接近下列哪個選項？（註：眼睛往下看目標物時,視線與水平線間的夾角稱為俯角）
(1) $150$
(2) $150\sin 22^{\circ}$
(3) $150\cos 22^{\circ}$
(4) $\frac{150}{\cos 22^{\circ}}$
(5) $\frac{150}{\sin 22^{\circ}}$

[單選]

答案

設繩索長度為 $l$,在由甲乙兩樓頂和水平距離構成的直角三角形中,水平距離為 $150$ 公尺,俯角為 $22^{\circ}$,繩索長度 $l$ 與水平距離的關系為 $\cos22^{\circ}=\frac{150}{l}$,則 $l=\frac{150}{\cos 22^{\circ}}$。答案：(4)

https://www.ceec.edu.tw/files/file_pool/1/0n045357541158913049/04-112%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

111學測數學B試題-19

18-20為題組
中國虎丘塔、護珠塔與義大利的比薩斜塔是三座著名斜塔,它們的塔高分別為$48$、$19$與$57$（公尺）,偏移距離分別為$2.3$、$2.3$與$4$（公尺）,塔的傾斜度分別記為$\theta_{1}^{\circ}$、$\theta_{2}^{\circ}$與$\theta_{3}^{\circ}$。試比較$\theta_{1}$、$\theta_{2}$與$\theta_{3}$三數的大小關係。

[非選擇]

答案

$\begin{align*}
&由「\frac{偏移距離}{塔高}=\sin\theta」，計算各角度對應的\sin\theta：\\
&\sin\theta_1^\circ=\frac{2.3}{48}\approx0.05，\\
&\sin\theta_2^\circ=\frac{2.3}{19}\approx0.12，\\
&\sin\theta_3^\circ=\frac{4}{57}\approx0.07。\\
\\
&因\sin\theta在(0^\circ,90^\circ)遞增，故\sin\theta_2^\circ>\sin\theta_3^\circ>\sin\theta_1^\circ \implies \theta_2>\theta_3>\theta_1。
\end{align*}$

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加最愛

Saved articles