快查考古題 > 圓的角度與弦弧

圓的角度與弦弧

Posted in

106學測數學考科–06

試問有多少個實數 \( x \) 滿足 \(\frac{\pi}{2} \leq x \leq \frac{3\pi}{2}\) 且 \(\cos x^0 \leq \cos x\)？
(1) 0 個
(2) 1 個
(3) 2 個
(4) 4 個
(5) 無窮多個。

[單選題]
答案

\(x^0\) 約介於 1.57° 與 4.71° 之間，\(\cos x^0 > 0\)。而 \(x\) 弧度在 \(\frac{\pi}{2}\) 到 \(\frac{3\pi}{2}\) 之間，\(\cos x \leq 0\)。故 \(\cos x^0 > \cos x\)，恆成立，無解。故選(1)。答案：(1)

加入最愛清單 加最愛
Posted in

109學測數學考科-G

設計師為天文館設計以不銹鋼片製成的月亮形狀，其中有一款設計圖如右圖所示：圖中，圓弧 \( QRT \) 是一個以 \( O \) 點為圓心、\( OT \) 為直徑的半圓，\( OT = 2\sqrt{3} \)。圓弧 \( QST \) 的圓心在 \( P \) 點，\( PQ = PT = 2 \)。圓弧 \( QRT \) 與圓弧 \( QST \) 所圈出的灰色區域 \( QRTSQ \) 即為某一天所見的月亮形狀。設此灰色區域的面積為 \( a\pi + \sqrt{b} \)，其中 \( \pi \) 為圓周率，\( a \) 為有理數，\( b \) 為整數，則 \( a = \) __________（化為最簡分數），\( b = \) __________。

[選填題]
答案

半圓QRT面積 = \(\frac{3\pi}{2}\)，扇形PQST面積 = \(\frac{4\pi}{3}\)，△PQT面積 = \(\sqrt{3}\)。灰色區域面積 = 半圓 + △PQT - 扇形 = \(\frac{1}{6}\pi + \sqrt{3}\)，故 \(a = \frac{1}{6}\), \(b = 3\)。答案：\(a = \frac{1}{6}, b = 3\)

加入最愛清單 加最愛
Posted in

114學測數學A考科_16

坐標平面上，設 \(L_1\)、\(L_2\) 為通過點 \((3, 1)\) 且斜率分別為 \(m\)、\(-m\) 的兩條直線，其中 \(m\) 為一實數。另設 \(\Gamma\) 為圓心在原點的一個圓。已知 \(\Gamma\) 與 \(L_1\) 交於相異兩點 \(A\)、\(B\)，且知圓心到 \(L_1\) 的距離為 1，又 \(\Gamma\) 與 \(L_2\) 相切，則弦 \(\overline{AB}\) 的長度為 __________。（化為最簡分數）

[選填題]
答案

圓 \(\Gamma: x^2+y^2=r^2\)，\(L_1: mx-y-3m+1=0\)，圓心到 \(L_1\) 距離為 1 得 \(m=\frac{3}{4}\)。
代入 \(L_2\) 與圓相切得 \(r=\frac{13}{5}\)，弦長 \(\overline{AB}=2\sqrt{r^2-1^2}=\frac{24}{5}\)。

加入最愛清單 加最愛
Posted in

107指考數學甲試題–A

坐標平面上，已知圓\(C\)通過點\(P(0,-5)\)，其圓心在\(x = 2\)上。若圓\(C\)截\(x\)軸所成之弦長為\(6\)，則其半徑為\(\sqrt{(\quad)}\)。(化成最簡根式)

[選填題]
答案

設圓\(C\)的圓心坐標為\((2,y_0)\)，半徑為\(r\)。
圓\(C\)截\(x\)軸所成之弦長為\(6\)，則弦長的一半為\(3\)。
圓心\((2,y_0)\)到\(x\)軸的距離為\(\vert y_0\vert\)。
根據勾股定理，\(r^{2}=3^{2}+\vert y_0\vert^{2}\)。
又因為圓\(C\)過點\(P(0,-5)\)，所以\((0 - 2)^{2}+(-5 - y_0)^{2}=r^{2}\)。
將\(r^{2}=3^{2}+\vert y_0\vert^{2}\)代入\((0 - 2)^{2}+(-5 - y_0)^{2}=r^{2}\)可得：
\(4 + (-5 - y_0)^{2}=9 + y_0^{2}\)
\(4 + 25 + 10y_0 + y_0^{2}=9 + y_0^{2}\)
\(10y_0=-20\)
解得\(y_0=-2\)。
所以\(r^{2}=3^{2}+(-2)^{2}=9 + 4 = 13\)，則\(r = \sqrt{13}\)。故答案為\(13\)。

加入最愛清單 加最愛
Posted in

111學測數學B試題-18

18-20 題為題組
瘦長的塔因為年代久遠，塔身容易傾斜。在下方右圖中，以粗黑線條代表塔身，而塔 身的長度稱為塔高，塔身與鉛直虛線的夾角稱為該塔的傾斜度（ $0\le 90$），又塔頂至鉛 直虛線的距離稱為該塔的偏移距離。
已知世界上傾斜度最高的摩天大樓坐落於阿布達比,其傾斜度達到\(18^{\circ}\),此傾斜度換算成弳（或弧度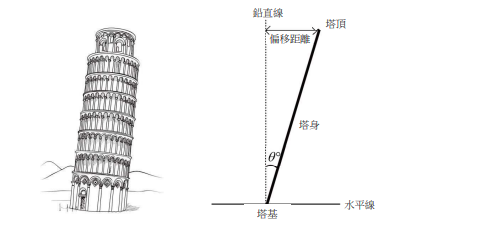）為下列哪一個選項？
(1) \(\frac{\pi}{36}\)；
(2) \(\frac{\pi}{18}\)；
(3) \(\frac{\pi}{20}\)；
(4) \(\frac{\pi}{10}\)；
(5) \(\frac{\pi}{8}\)

[單選]
答案

1. 因為\(180^{\circ}=\pi\)弧度,設\(18^{\circ}\)對應的弧度為\(x\)。
2. 則由比例關系可得\(\frac{180^{\circ}}{\pi}=\frac{18^{\circ}}{x}\)。
3. 解得\(x=\frac{18\pi}{180}=\frac{\pi}{10}\)。答案：(4)

https://www.ceec.edu.tw/files/file_pool/1/0m053363176747148935/04-111%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e9%81%b8%e6%93%87%28%e5%a1%ab%29%e9%a1%8c%e7%ad%94%e6%a1%88.pdf

加入最愛清單 加最愛