\(\triangle ABC\) 中,已知 \(\overline{AB} = \overline{BC} = 3\),\(\cos \angle ABC = -\frac{1}{8}\)。在 \(\triangle ABC\) 的外接圓上有一點 \(D\) 滿足 \(\overline{BD} = 4\),且 \(\overline{AD} \leq \overline{CD}\),則 \(\overline{CD} = \) __________。(化為最簡根式)
[選填題]平面幾何圖形
113學測數學A考科_06
在同一平面上,相距 \(7\) 公里的 \(A \cdot B\) 兩砲臺,\(A\) 在 \(B\) 的正東方。某次演習時,\(A\) 向西偏北 \(\theta\) 方向發射砲彈,\(B\) 則向東偏北 \(\theta\) 方向發射砲彈,其中 \(\theta\) 為銳角,觀測回報兩砲彈皆命中 9 公里外的同一目標 \(P\)。接著 \(A\) 改向西偏北 \(\frac{\theta}{2}\) 方向發射砲彈,彈著點為 \(9\) 公里外的點 \(Q\)。試問砲臺 \(B\) 與彈著點 \(Q\) 的距離 \(BQ\) 為何?
(1) 4 公里
(2) 4.5 公里
(3) 5 公里
(4) 5.5 公里
(5) 6 公里
113學測數學A考科_08
對任一正整數\(n\geq 2\),令\(T_n\)表示邊長為\(n,n+1,n+2\)的三角形。試選出正確的選項。
(1) \(T_n\)皆為銳角三角形
(2) \(T_2,T_3,T_4,\ldots,T_{10}\)的周長形成等差數列
(3) \(T_n\)的面積隨\(n\)增大而增大
(4) \(T_5\)的三高依序形成等差數列
(5) \(T_3\)的最大角大於\(T_2\)的最大角
113學測數學A考科_12
在坐標平面上給定三點 \(A(1,0), B(0,1), C(-1,0)\),令 \(\Gamma\) 為 \(\triangle ABC\) 經矩陣 \(T=\begin{bmatrix} 3 & 0 \\ a & 1 \end{bmatrix}\) 變換後的圖形,其中 \(a\) 為實數。試選出正確的選項。
(1) 若 \(a=0\),則 \(\Gamma\) 為等腰直角三角形
(2) \(\triangle ABC\) 的邊上至少有兩點經 \(T\) 變換後坐標不變
(3) \(\Gamma\) 必有部分落在第四象限
(4) 平面上找到一個圖形 \(\Omega\) 經 \(T\) 變換後為 \(\triangle ABC\)
(5) \(\Gamma\) 的面積為定值
107指考數學乙試題-非選擇一(1)
已知實係數二次多項式函數 \( y = f(x) \) 滿足 \( f(3) = f(-7) \)。試回答下列問題。
(1) 寫出 \( y = f(x) \) 圖形的對稱軸方程式。
109指考數學乙(補考)試題-02
在坐標平面上,\( O \) 為原點,考慮直線 \( L_1: 5x+3y=5 \) 與直線 \( L_2: 3x+2y=6-2a \),其中 \( a \) 為實數。若直線 \( L: 2x+y=3 \) 分別與直線 \( L_1 \) 及直線 \( L_2 \) 交於點 \( A \) 及點 \( B \),則三角形 \( OAB \) 的面積為下列哪一個選項?
(1) \( \frac{1}{2} |a-2| \)
(2) \( |a-2| \)
(3) \( 2|a-2| \)
(4) \( 3|a-2| \)
(5) \( 6|a-2| \)
求A點:解 \( \begin{cases} 5x+3y=5 \\ 2x+y=3 \end{cases} \),得 \( x=4 \),\( y=-5 \),故 \( A(4,-5) \)
求B點:解 \( \begin{cases} 3x+2y=6-2a \\ 2x+y=3 \end{cases} \),得 \( x=2a \),\( y=3-4a \),故 \( B(2a,3-4a) \)
三角形OAB面積 = \( \frac{1}{2} |x_A y_B - x_B y_A| = \frac{1}{2} |4(3-4a) - 2a(-5)| = \frac{1}{2} |12-16a+10a| = \frac{1}{2} |12-6a| = 3|2-a| = 3|a-2| \)
答案:(4)
114分科測驗數學乙考科試卷-08
平面上三角形ABC,\(\angle A=91^\circ\)、\(\angle C=29^\circ\),令\(\overline{BC}=a\)、\(\overline{CA}=b\)、\(\overline{AB}=c\),試選出正確的選項?
(1) \(a^2\gt b^2+c^2\)
(2) \(\frac{c}{a}\gt\sin29^\circ\)
(3) \(\frac{b}{a}\gt\cos29^\circ\)
(4) \(\frac{a^2+b^2-c^2}{ab}\lt\sqrt{3}\)
(5) 外接圓半徑小於c
已知三角形 \(ABC\) 中:
\[
\angle A = 91^\circ, \quad \angle C = 29^\circ, \quad \angle B = 60^\circ
\]
(因為 \(180^\circ - 91^\circ - 29^\circ = 60^\circ\))
邊長:
\[
BC = a, \quad CA = b, \quad AB = c
\]
(即 \(a\) 對 \(\angle A\),\(b\) 對 \(\angle B\),\(c\) 對 \(\angle C\))
---
**(1) \( a^2 > b^2 + c^2 \)**
由餘弦定理:
\[
a^2 = b^2 + c^2 - 2bc\cos A
\]
\(\cos 91^\circ < 0\),所以 \(-2bc\cos A > 0\),因此
\[
a^2 > b^2 + c^2
\]
✅ 正確。
---
**(2) \( \frac{c}{a} > \sin 29^\circ \)**
正弦定理:
\[
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R
\]
所以
\[
\frac{c}{a} = \frac{\sin C}{\sin A} = \frac{\sin 29^\circ}{\sin 91^\circ}
\]
\(\sin 91^\circ \approx \sin 90^\circ = 1\),實際略大於 1(\(\sin 91^\circ \approx 0.99985\)),所以
\[
\frac{c}{a} \approx 0.99985^{-1} \times \sin 29^\circ \approx 1.00015 \times 0.4848 \approx 0.48487
\]
而 \(\sin 29^\circ \approx 0.4848\),比較:
\[
\frac{c}{a} \approx 0.48487 > 0.4848
\]
✅ 正確(雖然很接近,但確實大於)。
---
**(3) \( \frac{b}{a} > \cos 29^\circ \)**
\[
\frac{b}{a} = \frac{\sin B}{\sin A} = \frac{\sin 60^\circ}{\sin 91^\circ} \approx \frac{0.866025}{0.99985} \approx 0.86615
\]
\(\cos 29^\circ \approx 0.87462\),比較:
\[
0.86615 < 0.87462
\]
❌ 錯誤。
---
**(4) \( \frac{a^2 + b^2 - c^2}{ab} < \sqrt{3} \)**
由餘弦定理:
\[
\cos C = \frac{a^2 + b^2 - c^2}{2ab}
\]
所以
\[
\frac{a^2 + b^2 - c^2}{ab} = 2\cos C = 2\cos 29^\circ \approx 2 \times 0.87462 \approx 1.74924
\]
\(\sqrt{3} \approx 1.732\),比較:
\[
1.74924 > 1.732
\]
❌ 錯誤。
---
**(5) 外接圓半徑小於 \(c\)**
外接圓半徑 \(R = \frac{a}{2\sin A} \approx \frac{a}{2 \times 0.99985} \approx 0.500075 \times a\)
由正弦定理:
\[
c = 2R \sin C \implies R = \frac{c}{2\sin C} = \frac{c}{2 \times 0.4848} \approx \frac{c}{0.9696} \approx 1.0314 \times c
\]
等等,這裡要小心:題目給的 \(a,b,c\) 是邊長,\(R\) 是固定值。
用 \(a = 2R\sin A\),\(c = 2R\sin C\)。
比較 \(R\) 與 \(c\):
\[
c = 2R\sin C \implies \frac{R}{c} = \frac{1}{2\sin C} \approx \frac{1}{0.9696} \approx 1.0314
\]
所以 \(R \approx 1.0314 \times c > c\),因此 \(R < c\) 不成立。
❌ 錯誤。
---
**正確選項:** (1)、(2)
\[
\boxed{12}
\]
114分科測驗數學甲試卷-06
設指數函數 \(f(x)=1.2^x\)。試選出正確的選項?
(1) \(f(0)\gt0\)
(2) \(f(10)\gt10\)
(3) 坐標平面上,\(y=1.2^x\) 的圖形與直線 \(y=x\) 相交
(4) 坐標平面上,\(y=1.2^x\) 與 \(y=\log(1.2^x)\) 的圖形對稱於直線 \(y=x\)
(5) 對任意正實數 \(b,\log_{1.2}b \neq1.2^b\)
106指考數學甲試題–B
坐標平面上有三條直線\(L\)、\(L_1\)、\(L_2\),其中\(L\)為水平線,\(L_1\)、\(L_2\)的斜率分別為\(\frac{3}{4}\)、\(-\frac{4}{3}\)。已知\(L\)被\(L_1\)、\(L_2\)所截出的線段長為30,則\(L\)、\(L_1\)、\(L_2\)所決定的三角形的面積為____。
[選填題]設直線 \( L: y = k \),與 \( L_1: 3x-4y=0 \)、\( L_2: 4x+3y=0 \) 的交點分別為 \( A、B \):
- 代入 \( L_1 \) 得 \( A\left(\frac{4k}{3}, k\right) \);
- 代入 \( L_2 \) 得 \( B\left(-\frac{3k}{4}, k\right) \)。
計算 \( \overline{AB} \) 的長度:
\[
\overline{AB} = \frac{4k}{3} - \left(-\frac{3k}{4}\right) = \frac{25k}{12}
\]
由 \( \overline{AB}=30 \),得:
\[
\frac{25k}{12}=30 \implies k=\frac{72}{5}
\]
故 \( \triangle OAB \) 的面積為:
\[
\text{面積} = \frac{1}{2} \times \overline{AB} \times k = \frac{1}{2} \times 30 \times \frac{72}{5} = 216
\]
106指考數學甲試題-非選擇二(1)
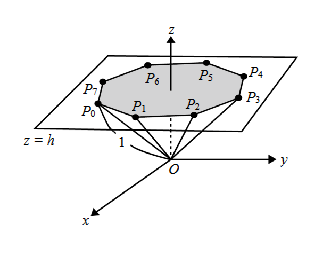
坐標空間中,\(O(0,0,0)\)為原點。平面\(z = h\)(其中\(0\leq h\leq1\))上有一以\((0,0,h)\)為圓心的圓,在此圓上依逆時針順序取8點構成正八邊形\(P_0P_1P_2P_3P_4P_5P_6P_7\),使得各線段\(\overline{OP_j}(0\leq j\leq7)\)的長度都是1。試以\(h\)表示向量內積\(\overrightarrow{OP_0}\cdot\overrightarrow{OP_4}\)。(4分)
[非選擇題]在平面\(z = h\)上,以\((0,0,h)\)為圓心,半徑\(r=\sqrt{1 - h^{2}}\)(由\(\vert\overrightarrow{OP_j}\vert = 1\),根據勾股定理可得)。
將正八邊形放置在平面\(z = h\)上,以圓心\((0,0,h)\)為中心建立平面直角坐標系(在\(z = h\)這個平面內)。
對於正八邊形,相鄰兩邊夾角為\(\frac{360^{\circ}}{8}=45^{\circ}\),\(\overrightarrow{OP_0}\)與\(\overrightarrow{OP_4}\)的夾角為\(4\times45^{\circ}=180^{\circ}\)。
設\(\overrightarrow{OP_0}=(x_1,y_1,h)\),\(\overrightarrow{OP_4}=(x_2,y_2,h)\),由\(\vert\overrightarrow{OP_0}\vert=\vert\overrightarrow{OP_4}\vert = 1\),可得\(x_1^{2}+y_1^{2}+h^{2}=1\),\(x_2^{2}+y_2^{2}+h^{2}=1\)。
\(\overrightarrow{OP_0}\cdot\overrightarrow{OP_4}=x_1x_2 + y_1y_2+h^{2}\)。
在平面\(z = h\)上,\(\overrightarrow{OP_0}\)與\(\overrightarrow{OP_4}\)的向量關係可根據正八邊形的旋轉性質得到。
由正八邊形性質可知,\(\overrightarrow{OP_0}\)與\(\overrightarrow{OP_4}\)在\(z = h\)平面上的投影向量大小相等,方向相反(夾角\(180^{\circ}\)),且投影向量模長\(r=\sqrt{1 - h^{2}}\)。
所以\(\overrightarrow{OP_0}\cdot\overrightarrow{OP_4}=- (1 - h^{2})+h^{2}=2h^{2}-1\)。