設\(x_{0}\)、\(y_{0}\)為正實數。若坐標平面上的點\((10x_{0},100y_{0})\)在函數\(y = 10^{x}\)的圖形上,則點\((x_{0},\log y_{0})\)會在直線\(y = ax + b\)的圖形上,其中\(a\)、\(b\)為實數。試問\(2a – b\)的值為何?
(1)\(4\)
(2)\(9\)
(3)\(15\)
(4)\(18\)
(5)\(22\)
指數與對數
112分科測驗數學甲考科試題-02
放射性物質的半衰期T定義為「每經過時間T,該物質的質量會衰退成原來的一半」。鉛製容器中有A、B兩種放射性物質,其半衰期分別為 \( T_A \)、\( T_B \)。開始記錄時這兩種物質的質量相等,112天後測量發現物質B的質量為物質A的質量的四分之一。根據上述,試問 \( T_A \)、\( T_B \) 滿足下列哪一個關係式?
(1) \(-2 + \frac{112}{T_A} = \frac{112}{T_B}\)
(2) \(2 + \frac{112}{T_A} = \frac{112}{T_B}\)
(3) \(-2 + \log_2 \frac{112}{T_A} = \log_2 \frac{112}{T_B}\)
(4) \(2 + \log_2 \frac{112}{T_A} = \log_2 \frac{112}{T_B}\)
(5) \(2 \log_2 \frac{112}{T_A} = \log_2 \frac{112}{T_B}\)
設初始質量為 \(M\),112天後A的質量為 \(M \cdot 2^{-\frac{112}{T_A}}\),B的質量為 \(M \cdot 2^{-\frac{112}{T_B}}\)。根據題意,\(M \cdot 2^{-\frac{112}{T_B}} = \frac{1}{4} M \cdot 2^{-\frac{112}{T_A}}\),即 \(2^{-\frac{112}{T_B}} = 2^{-2} \cdot 2^{-\frac{112}{T_A}}\)。取對數得 \(-\frac{112}{T_B} = -2 - \frac{112}{T_A}\),整理得 \(2 + \frac{112}{T_A} = \frac{112}{T_B}\)。答案為(2)。
111分科數學甲試題-01
設\(a_{1}\),\(a_{2}\),\(a_{3}\),\(a_{4}\)是首項為10、公比是10的等比數列。令\(b = \sum\limits_{n = 1}^{3}\log_{a_{n}}a_{n + 1}\) ,試選出\(b\)的範圍。
(1)\(2 < b\leqslant3\)
(2)\(3 < b\leqslant4\)
(3)\(4 < b\leqslant5\)
(4)\(5 < b\leqslant6\)
(5)\(6 < b\leqslant7\)
由等比數列通項公式\(a_{n}=a_{1}q^{n - 1}\)(此處\(a_{1}=10\),\(q = 10\))可得\(a_{n}=10^{n}\)。
則\(b=\log_{a_{1}}a_{2}+\log_{a_{2}}a_{3}+\log_{a_{3}}a_{4}=\log_{10}10^{2}+\log_{10^{2}}10^{3}+\log_{10^{3}}10^{4}\)。
根據換底公式\(\log_{m}n=\frac{\log_{k}n}{\log_{k}m}\),可化簡為\(b = 2+\frac{3}{2}+\frac{4}{3}=\frac{12 + 9 + 8}{6}=\frac{29}{6}\approx4.83\) ,所以\(4 < b\leqslant5\) ,答案為(3)。
113分科測驗數學甲試題11
設 實數 \( a_{1},a_{2},\cdots,a_{9} \) 是 公差為 \( 2 \) 的 等 差 數列 ,其中 \( a_{1}\neq0\) 且 \( a_{3}>0\)。若 \(\log_{2}a_{3},\log_{2}b,\log_{2}a_{9}\) 三數依序也成等差數列 ,其中 \( b \) 為 \( a_{4},a_{5},a_{6},a_{7},a_{8} \) 其中一數,則 \(a_9 =\)__________ 。
[選填]已知\(\{a_n\}\)是公差\(d = 2\)的等差數列,則\(a_n = a_1 + 2(n - 1)\)。由\(\log_2 a_3, \log_2 b, \log_2 a_9\)成等差數列,得\(2\log_2 b = \log_2 a_3 + \log_2 a_9\),即\(b^2 = a_3 a_9\)。計算\(a_3 = a_1 + 4\),\(a_9 = a_1 + 16\),代入\(b^2 = (a_1 + 4)(a_1 + 16)\)。因b為\(a_4, a_5, a_6, a_7, a_8\)之一,逐一驗證:若\(b = a_4 = a_1 + 6\),則\((a_1 + 6)^2 = (a_1 + 4)(a_1 + 16)\),展開得:\(a_1^2 + 12a_1 + 36 = a_1^2 + 20a_1 + 64 \implies -8a_1 = 28 \implies a_1 = -\frac{7}{2}\)
此時\(a_3 = -\frac{7}{2} + 4 = \frac{1}{2} > 0\),符合條件。因此,\(a_9 = a_1 + 16 = -\frac{7}{2} + 16 = \frac{25}{2}\)。最終答案:\(\boxed{\dfrac{25}{2}}\)
114學測數學B試題03
已知實數 \( a,b \) 滿足 \( \frac{1}{2} \lt a \lt 1 \) 及 \( 1 \lt b \lt 2 \)。試問下列哪個選項的值最小?
(1) 0
(2) \( \log a \)
(3) \( \log(a^2) \)
(4) \( \log b \)
(5) \( \frac{1}{\log b} \)
1. 分析選項(2):
因 \( \frac{1}{2} < a < 1 \),對數函數 \( y = \log x \)(以10或自然對數為底,底數>1)在\( (0,1) \)上為負,故 \( \log a < 0 \)。
2. 分析選項(3):
\( \log(a^2) = 2\log a \),因 \( \log a < 0 \),故 \( 2\log a < \log a \)(負數乘以2更小)。
3. 分析選項(4):
因 \( 1 < b < 2 \),故 \( \log b > 0 \)。
4. 分析選項(5):
因 \( \log b > 0 \),故 \( \frac{1}{\log b} > 0 \)。
5. 比較選項(2)與(3):
令 \( a = \frac{\sqrt{2}}{2} \)(滿足 \( \frac{1}{2} < a < 1 \)),則 \( \log a = \log \frac{\sqrt{2}}{2} = \frac{1}{2}\log 2 - \log 2 = -\frac{1}{2}\log 2 \),\( \log(a^2) = 2 \times (-\frac{1}{2}\log 2) = -\log 2 \)。
因 \( -\log 2 < -\frac{1}{2}\log 2 \),故 \( \log(a^2) < \log a \)。
综上,選項(3)的值最小。"
https://www.ceec.edu.tw/files/file_pool/1/0p051541901400830673/04-114%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e7%ad%94%e6%a1%88.pdf
114學測數學B試題18
地球受到太陽照射過來的紫外線強度以\(UVI\)數值表示, 一單位\(UVI\)的照射強度相當於每平方公尺\(100\)焦耳的能量。已知\(UVI\)數值與所在高度呈指數關係: 高度每上升\(300\)公尺,其\(UVI\)數值增加上升前的\(4\%\)。在地平面上接收到太陽發出每平方公尺\(400\)焦耳的紫外線,則到了離地平面\(4500\)公尺高的山上,接收到紫外線的\(UVI\)數值為下列哪一個選項?(1) \(4(1 + 0.04×15)\);(2) \(4(1 + 0.04^{15})\);(3) \(4(1 + 0.04)^{15}\);(4) \(4×100(1 + 0.04)^{15}\);(5) \(4×100(1 + 0.04^{45})\)
[單選]地平面上能量\(400\)焦耳,則\(UVI\)數值為\(4\)。高度上升\(4500\)公尺,\(4500÷300 = 15\),即經過\(15\)次\(300\)公尺上升,每次增加\(4\%\),所以\(UVI\)數值為\(4(1 + 0.04)^{15}\)。答案:(3)
https://www.ceec.edu.tw/files/file_pool/1/0p051541901400830673/04-114%e5%ad%b8%e6%b8%ac%e6%95%b8%e5%ad%b8b%e7%ad%94%e6%a1%88.pdf
113學測數學B試題-02
已知\(a\),\(b\),\(c\)為實數,且滿足\(1\lt a\lt10\)、\(b = \log a\)、\(c = \log b\),試選出正確的選項。
(1) \(c\lt0\lt b\lt1\);
(2) \(0\lt c\lt1\lt b\);
(3) \(0\lt c\lt b\lt1\);
(4) \(1\lt c\lt b\);
(5) \(c\lt b\lt0\)
1. 已知\(1\lt a\lt10\),對於\(y = \log x\)(假設以\(10\)為底),當\(x = a\)時,\(b=\log a\),由對數函數性質可得\(0\lt\log a\lt1\),即\(0\lt b\lt1\)。
2. 又\(c = \log b\),因為\(0\lt b\lt1\),所以\(\log b\lt0\),即\(c\lt0\)。所以\(c\lt0\lt b\lt1\)。答案:(1)
113學測數學B試題18
[題組說明18-20]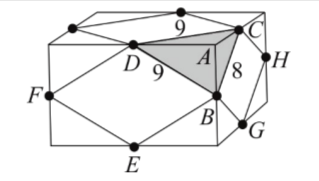
如右圖所示,考慮長方體的石塊上某一頂點 \( A \) 及包含點 \( A \) 的一個面,令這個面的各邊中點分別為 \( B, E, F, D \)。此長方體上包含點 \( B \) 的另一個面,令其各邊中點分別為 \( B, C, H, G \)。已知 \( \overline{BC} = 8 \),\( \overline{BD} = \overline{DC} = 9 \)。現將此石塊截去八個角,使得每個截角的截面恰通過該截角之三鄰邊的中點。根據上述,試回答下列問題。
18.] 截角後的石塊為幾面體?(單選題,3 分)
(1) 八面體
(2) 十面體
(3) 十二面體
(4) 十四面體
(5) 十六面體
$\textbf{答 案:(4)}$
