在1952年的第一次氫彈試爆中,首次發現了原子序99的鎧(Es)元素,已知此人造元素同位素Es-253的半生期為20.5天。若是能取得0.20 mg的Es-253,立即與配位基進行合成及鈉化,得到的錐合物產率為70%,經過10天後,則此錐合物中含有黃變後殘餘的Es-253量約為多少(mg)?
(A) 0.18
(B) 0.16
(C) 0.14
(D) 0.12
(E) 0.10
數量關係計算
110指考物理分科考科_02
假設在水波槽中,與水波波速可能有關的物理量為重力加速度 \( g \)、水的密度 \( \rho \) 與水深 \( D \)。若僅以上述三個物理量的因次來判斷波速 v,則下列何者正確?
(A) v 正比於 \( gD \)
(B) v 正比於 \( \rho gD \)
(C) v 正比於 \( \sqrt{gD} \)
(D) v 正比於 \( g\sqrt{\rho D} \)
(E) v 正比於 \( \frac{1}{\sqrt{gD}} \)。
110指考物理分科考科_03
[題組:第3-4題]
假設棒球的旋轉與空氣阻力可被忽略,回答第3-4題有關棒球的問題。
某職棒投手先以固定力將靜止的棒球沿直線帶動約 1.5 m 的長度後,投出 144 km/h 的快速直球。已知棒球的質量約為 150 g,則該投手施於球的固定力量值約為何?
(A) 80 N
(B) 100 N
(C) 110 N
(D) 120 N
(E) 130 N。
110指考物理分科考科_04
[題組:第3-4題]
棒球抵達本壘板上方時,在離地 1.0 m 的高度,被打擊者以與水平面夾角為 \( \theta (\cos \theta = \frac{3}{5}) \) 的仰角,量值為 126 km/h 的速度反向擊出,該球在被擊出後 5.0 s 恰好飛越全壘打牆的上空,試問球飛越全壘打牆瞬間,離地高度為多少 m?(假設棒球場地面為水平,取重力加速度 \( g = 10 \text{m/s}^2 \))
(A) 4
(B) 8
(C) 10
(D) 12
(E) 16。
略解:\( v_0 = 126 \text{km/h} = 35 \text{m/s} \),\( \cos \theta = \frac{3}{5} \),\( \sin \theta = \frac{4}{5} \)。
鉛直位移:\( y = v_{0y} t - \frac{1}{2}gt^2 = 35 \times \frac{4}{5} \times 5 - \frac{1}{2} \times 10 \times 5^2 = 140 - 125 = 15 \text{m} \)。
離地高度:\( 1.0 + 15 = 16 \text{m} \)。
答案:E
110指考物理分科考科_07
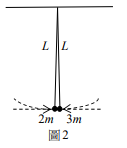
有兩顆大小相同的小球,各以長度為L、質量可忽略不計的擺錘掛在天花板同一點,左邊小球的質量為 \( 2m \),右邊小球的質量為 \( 3m \)。某生拉起兩小球至高度分別為 \( h_L \) 和 \( h_R \),將小球由靜止釋放,讓小球擺向中間,使兩小球恰在最低點時發生正向彈性碰撞,如圖2所示。碰撞後,若左邊的小球擺回到最高點的高度仍然為 \( h_L \),則 \( h_L : h_R \) 為何?
(A)9:4
(B)3:2
(C)1:1
(D)2:3
(E)4:9
略解:碰撞前速率:\( v_{2m} = \sqrt{2gh_L} \),\( v_{3m} = -\sqrt{2gh_R} \)(設向右為正)。
彈性碰撞後,左球速度:
\( v_{2m}' = \frac{2m-3m}{2m+3m} \sqrt{2gh_L} + \frac{2 \times 3m}{2m+3m} (-\sqrt{2gh_R}) = -\frac{1}{5} \sqrt{2gh_L} - \frac{6}{5} \sqrt{2gh_R} \)。
題意 \( v_{2m}' = -\sqrt{2gh_L} \),故 \( -\sqrt{h_L} = -\frac{1}{5} \sqrt{h_L} - \frac{6}{5} \sqrt{h_R} \Rightarrow \frac{4}{5} \sqrt{h_L} = \frac{6}{5} \sqrt{h_R} \Rightarrow \sqrt{h_L} : \sqrt{h_R} = 3:2 \Rightarrow h_L : h_R = 9:4 \)。
答案:A
110指考物理分科考科_09
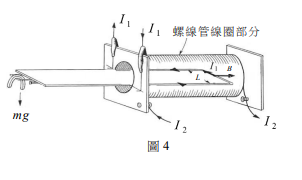
圖4為電流天平的構造示意圖。當U型電路上的電流值為 \( I_1 \)、螺線管所載電流值為 \( I_2 \)、天平左端所掛的小重物質量為 \( m \) 時,天平恰成平衡。若將電流 \( I_1 \) 變成 \(-4I_1\),同時 \( I_2 \) 變成 \(-\frac{1}{2} I_2\)(負號表示電流方向與原來的方向相反),則此時可使天平平衡的小重物質量應為何?(忽略地磁造成的影響:g為重力加速度,L為U型電路寬度,B為螺線管所產生的磁場)
(A) \( m \)
(B) \( 2m \)
(C) \( 4m \)
(D) \( 8m \)
(E)天平無法達到平衡。
110指考物理分科考科_13
兩個點光源 \( S_1 \)、\( S_2 \) 間的距離為 24 cm,使用焦距為 9 cm 的薄透鏡 L,垂直放置於兩點光源 \( S_1 \)、\( S_2 \) 的連線上並調整位置,如圖 8 所示,使兩個點光源成像於同一位置,則兩點光源到透鏡的距離比為何?
(A) 3:4 (B) 3:8 (C) 2:3 (D) 1:2 (E) 1:3。
[單選題]略解:設 \( S_1 \)、\( S_2 \) 到透鏡距離為 \( p \)、\( 24-p \),成像於同一位置,則一為實像,一為虛像。
薄透鏡公式 \( \frac{1}{p} + \frac{1}{q} = \frac{1}{f} \)。
對 \( S_1 \):\( \frac{1}{p} + \frac{1}{q} = \frac{1}{9} \)。
對 \( S_2 \):\( \frac{1}{24-p} - \frac{1}{q} = \frac{1}{9} \)(虛像,q 取負)。
相加得 \( \frac{1}{p} + \frac{1}{24-p} = \frac{2}{9} \Rightarrow \frac{24}{p(24-p)} = \frac{2}{9} \Rightarrow p(24-p)=108 \)。
解 \( p^2 - 24p + 108 = 0 \Rightarrow (p-6)(p-18)=0 \Rightarrow p=6 \) 或 18。
距離比 6:18 = 1:3。
答案:E
110指考物理分科考科_19
在核電廠發生重大核安事故後,附近可檢測出放射性元素鈾-137,鈾-137自發衰變時,核子數減少至原來數目一半所需時間(半衰期)約為30年。已知每1g鈾-137的放射性活度約為 \(3.2 \times 10^{12} \text{Bq}\)(\(Bq\)為放射性活度的單位,\(1 \text{Bq}\)=每秒發生一次衰變;活度亦稱活性);食品中放射性鈾檢驗的容許量標準值為100 \(\text{Bq/kg}\)。
假設一尾100 kg的大型海魚在15年前體內的放射性物質只有 \(2.0 \times 10^{-8} \text{g}\)的放射性鈾-137,現今對其殘留的鈾-137進行檢驗,若鈾-137在這期間未被代謝出體外,則其每公斤的放射性活度為食品檢驗容許量之標準值的幾倍?
(A)0.045 (B)0.32 (C)4.5 (D)32 (E)450。
略解:經過15年為半衰期30年的一半,殘留質量 \( m = 2.0\times10^{-8} \times (\frac{1}{2})^{1/2} = \sqrt{2} \times 10^{-8} \text{g} \)。
活度 \( A = m \times 3.2\times10^{12} = \sqrt{2} \times 10^{-8} \times 3.2\times10^{12} \approx 1.414 \times 3.2 \times 10^4 = 4.5248 \times 10^4 \text{Bq} \)。
魚總活度 \( 4.5248\times10^4 \text{Bq} \),每公斤活度 \( \frac{4.5248\times10^4}{100} = 452.48 \text{Bq/kg} \)。
容許標準 100 Bq/kg,倍數 \( \frac{452.48}{100} \approx 4.5 \)。
答案:C
113物理分科測驗20
[題組:19-20題]
20 風機所標示的「額定功率」通常為風速12m/s時運轉的功率。近五年來臺灣平均每發100度電的二氧化碳排放量約為50kg。以一座額定功率為8kW的風機來發電,若全年中有1/3的時間風速皆為6m/s,另外2/3的時間風速皆為9m/s,則下列敘述哪些正確?
(1年有8760小時;1度電=1kW·h)(多選)(5分)
(A)當風速為6m/s時,該風機功率為12m/s風速額定功率時的1/4
(B)當風速為9m/s時,該風機功率為12m/s風速額定功率時的27/64
(C)若該風機全年以額定功率發電,則1年發電量為70080度
(D)該風機1年實際發電量為19710度
(E)在相同發電量下,該風機1年實際發電比臺灣近五年平均發電,約可減少11315kg的二氧化碳排放量
功率 \(P \propto v^3\)。
(A)錯:6m/s為12m/s之1/2,功率比為 \((1/2)^3=1/8\)。
(B)對:9m/s為12m/s之3/4,功率比為 \((3/4)^3=27/64\)。
(C)對:額定發電 \(E=8\times8760=70080 \text{度}\)。
(D)錯:實際發電 \(E=1\times(1/3\times8760) + (27/8)\times(2/3\times8760) = 2920+19710=22630 \text{度}\)。
(E)對:減排量 \(\frac{22630}{100}\times50=11315 \text{kg}\)。故選(B)(C)(E)。答案:BCE
114學測自然考科48
[題組:第47題到第49題]
假設 \( n_{內} \) 與 \( n_{外} \) 維持恆定,則在攝氏27度時的平衡電壓量值約是在攝氏17度時的多少倍?
(A) \(\frac{27}{17}\)
(B) \(\frac{17}{27}\)
(C) \(\frac{300}{290}\)
(D) \(\frac{290}{300}\)
(E) \(\frac{38}{36}\)