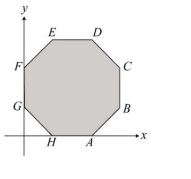
一線性規劃問題的可行解區域為坐標平面上的正八邊形 \(ABCDEFGH\) 及其內部,如右圖。已知目標函數 \(ax + by + 3\)(其中 \(a, b\) 為實數)的最大值只發生在 \(B\) 點。請問當目標函數改為 \(3bx – ay\) 時,最大值會發生在下列哪一點?
(1) \(A\)
(2) \(B\)
(3) \(C\)
(4) \(D\)
(5) \(E\)
由題意知 \( \overline{AB} \) 之斜率為 1(∵ \( \angle BAH = 135^\circ \))。
∵ 目標函數 \( ax + by + 3 \) 之最大值發生在 \( B \) 點,
∴ 斜率 \( -\dfrac{a}{b} > 1 \),即 \( \dfrac{a}{b} < -1 \)(亦即 \( \dfrac{b}{a} > -1 \))。
又目標函數改為 \( 3 - bx - ay \) 時,其斜率為 \( 0 < -\dfrac{b}{a} < 1 \)。 ∴ \( 3 - bx - ay \) 之最大值會發生在 \( A \) 點。 故選 (1)。