快查考古題 > 聲波

聲波

Posted in

110指考物理分科考科_08

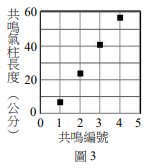
在聲速為350 m/s的環境中，進行音叉與氣柱的共鳴實驗。從零開始，逐漸增加氣柱長度，並將測得共鳴時的氣柱長度，依時間的先後順序編號為1、2、3、4，四次測得之共鳴氣柱長度對編號作圖，如圖3所示。實驗所用的音叉頻率，最接近多少Hz？
(A)350
(B)525
(C)700
(D)1050
(E)2000

[單選題]
答案

略解：圖中氣柱長約 8, 24, 40, 56 cm，為一端開口一端閉管。
相鄰共鳴長度差 \( \frac{\lambda}{2} = 24 - 8 = 16 \text{cm} \Rightarrow \lambda = 32 \text{cm} = 0.32 \text{m} \)。
\( f = \frac{v}{\lambda} = \frac{350}{0.32} = 1093.75 \text{Hz} \)，最接近 1050 Hz。
答案：D

加入最愛清單 加最愛
Posted in

111物理分科測驗–25

[題組:第25題到第26題] 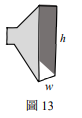◎聲波和光波一樣，在通過狹隘的開口往前傳播時都會出現繞射現象，而適用相同的繞射公式。圖13的矩形喇叭筒擴音器，是瑞士發明的，目的是在起大霧時，使喊話或警報能傳播到海岸邊一個大角度扇形水平區域內的船隻，避免將聲波能量浪費於向上或向下的傳播，w與h分別代表矩形開口的寬度與高度。當波發生繞射時，波強度出現極小值的角度θ，與波長λ和狹縫寬度的關係為 \( a \sin θ = nλ \quad (0 ≤ θ ≤ 90°, n = 1,2,3,\cdots) \) (1)式。比起光波，聲波的波長λ與狹縫寬度的比值通常較接近於1，因此上式不易出現n > 1的情況，以致聲波由開口向外傳播時主要會分布在張角為2θ的角度內，此處 \( \sin θ = \frac{λ}{a} \)，而張角是指以開口為頂點所張的角度。當 \( \frac{λ}{a} > 1 \) 時，(1)式無解，表示開口就近似於一個點，其向外傳播之聲波在開口前方的分布範圍（即張角），可達到180°。
已知人大力喊話時，主要不是透過基頻而是透過頻率約3kHz的泛音與噪音傳送資訊。而近似為矩形擴音器時，人的嘴巴相當於寬度約6cm的開口。若聲速為340m/s，則人張口大力喊話時，在其前方可涵蓋的水平扇形區域，其張角最接近下列何者？（單選）
(A)20° (B)30° (C)50° (D)90° (E)180°

[題組題]
答案

波長 \( λ = \frac{v}{f} = \frac{340}{3000} ≈ 0.113 \) m。開口寬度 a = 0.06 m，\( \frac{λ}{a} = \frac{0.113}{0.06} ≈ 1.88 > 1 \)，故張角為180°，選(E)。

加入最愛清單 加最愛
Posted in

111物理分科測驗–26

[題組:第25題到第26題] (1)依據瑞立矩形開口擴音器的目的與聲波傳播的特性，建構一個關於瑞立矩形開口擴音器如何工作的理論模型，亦即說明該擴音器的寬度w與高度h，各與聲波波長λ具有什麼關係（需列出關係式），並預測要使聲波在水平方向的分散角度大於垂直方向的分散角度，w與h的大小關係應為何。（3分）
(2)承(1)：若要驗證該擴音器可達到聲音在水平與垂直方向的分散效果，在固定擴音器寬度w與高度h的情況下，需要測量何種數據？答題時若用到數學式或圖形，須說明所用各符號的定義。（3分）

[題組題]
答案

(1)由繞射公式 \( \sinθ = \frac{λ}{a} \)，水平分散角 \( 2θ_1 \)，垂直分散角 \( 2θ_2 \)。要使水平分散角大於垂直分散角，需 \( θ_1 > θ_2 \Rightarrow \frac{λ}{w} > \frac{λ}{h} \Rightarrow w < h \)。
(2)在距離擴音器L處測量聲音強度，在水平面上移動測量極小聲位置距離x，得 \( θ_1 = \tan^{-1}(\frac{x}{L}) \)；在垂直面上同理得 \( θ_2 \)。比較 \( θ_1 \) 和 \( θ_2 \) 即可驗證分散效果。

加入最愛清單 加最愛
Posted in

108學測自然試題-23

國樂音階的五音與頻率的對應如表 1 所示。
表 1

國樂音階 宮 商 角 徵 羽
頻率（Hz） 262 294 330 392 440

經測得「角」音在室溫空氣中傳播時的波長約為103公分。若五音的聲波都在相同狀況的空氣中傳播，則下列有關表1國樂五音的敘述，哪些正確？（應選2項）
(A)「宮」音聲波的傳播速率最慢
(B)「商」音聲波不會發生干涉現象
(C)五音的聲波均會發生繞射現象
(D)在室溫空氣中傳播時，「徵」音的聲波波長較「角」音為長
(E)在室溫空氣中傳播時，「羽」音聲波的波長約為77.3公分

[多選題]
答案

同介質波速相同(A錯)。任何聲波都能干涉、繞射(B錯，C對)。波長λ=v/f，頻率高則波長短。角音f=330Hz， λ=1.03m， v=λf≈340 m/s。羽音f=440Hz， λ=v/f=340/440≈0.773m=77.3cm(E對)。徵音f=392Hz > 角音330Hz，故波長較短(D錯)。故(C)(E)正確。

加入最愛清單 加最愛
Posted in

110學測自然試卷_17

科學家搭乘潛艇在臺灣東部海域下潛至約四千公尺的深海環境，觀察海水基本性質。已知聲速大小與溫度、鹽度、壓力成正比，下列圖片的變化趨勢何者正確？

[單選題]
答案

海水溫度隨深度增加而降低(表層暖，深層冷)。壓力隨深度增加而增加。密度隨深度增加而增加。答案：(E)

加入最愛清單 加最愛
Posted in

110學測自然試卷_34

如圖9，一輛車在無風的平地，沿著圓直徑由a往b行駛。當通過圓心O的瞬間，車上聲源發出壓時短暫、頻率為\( f_0 \)的聲波。若直徑cd與ab垂直，且靜立於a、b、c、d的四位聽者聽到的聲音頻率分別為\( f_a \)、\( f_b \)、\( f_c \)、\( f_d \)，則下列關係式哪些正確？（應選2 項）
(A) \( f_a = f_c \)
(B) \( f_a > f_d \)
(C) \( f_c = f_d \)
(D) \( f_b > f_a > f_c \)
(E) \( f_b > f_0 > f_a \)

[多選題]
答案

車向a移動，a聽到頻率增加(f_a>f_0)。車遠離b，b聽到頻率減少(f_b

加入最愛清單 加最愛
Posted in

112學測自然試卷_32

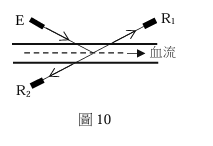
甲生為了利用都卜勒效應測量血流的速率，使一發射器 E 發出頻率 f 很高的聲波，斜向入射到血管中。聲波在被隨著血液流動的紅血球反射後，傳播到靜置於血管兩側的接收器 R1 和 R2 ，其中 R1 與發射器在血管同側，而 R2 在血管另一側，如圖 10 所示。若以 f1 和 f2 分別代表 R1 和 R2 測得的反射波頻率，則下列關係式，何者正確？
(A) f₁ = f₂
(B) f₂ < f
(C) f₂ = f
(D) f₁ < f₂
(E) f₁ = f < f₂

[單選題]
答案

對R₁：聲波先追近紅血球（頻率增加），再反射回R₁（頻率再增加），f₁ > f。對R₂：聲波遠離紅血球（頻率減少），再反射向R₂（頻率再減少），f₂ < f。故f₁ > f > f₂，(D)正確

加入最愛清單 加最愛